Problème à deux corps - Définition

Introduction

étoile binaire

Le problème à deux corps, ou mouvement képlerien est un point de départ de la mécanique classique, et un sujet essentiel de la mécanique céleste. Il concerne l'étude du mouvement relatif de deux points matériels M₁ et M₂ affectés de masses respectives m₁ et m₂ en interaction gravitationnelle. La solution était connue de Newton, qui a énoncé la loi fondamentale de la mécanique classique : le résultat est annoncé dans les propositions 57 à 65 de ses Principia.

Si le système est supposé isolé dans l'espace, les points M₁ et M₂ décrivent par rapport au centre de masse des ellipses homothétiques dont l'un des foyers est le centre de masse. Les caractéristiques (excentricité, position du second foyer) s'expriment en fonction de la masse réduite μ et de la masse totale. Ce résultat, loin d'être scolaire, est employé dans la détection des planètes extrasolaires.

Brève explication

On pose :

• 
• la force de M₁ sur M₂
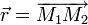
• C le centre de masse de M₁ et M₂

où m₁,m₂ sont les masses respectives des points M₁,M₂

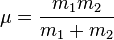
On définit alors un point fictif M appelé mobile réduit de masse μ et dont la position est définie par : . Les propriétés suivantes sont alors vérifiées :

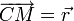
• le point M subit la force . En effet, le principe fondamental de la dynamique est vérifié :
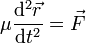
• La quantité de mouvement de M vaut

Le problème est donc ramené à un mouvement à force centrale, qui a été largement étudié.

Observations astronomiques

Pluton et Charon donnent, dans le système solaire, un bon exemple de couple où les deux membres sont de taille différente, mais aucun n'est négligeable devant l'autre. Le système plutonien comprend deux autres corps, mais leur influence est négligeable par rapport aux deux plus gros.

On observe qu'il existe des couples d'étoiles binaires.

Autre méthode

On décide d'étudier le mouvement de M2 dans le référentiel accéléré en translation d'origine M1 : il faut rajouter à la force centrale F(de1/2), la force d'inertie centrale -M2 a1 .

Or :

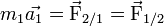
Donc le PFD s'écrit :  ; soit .

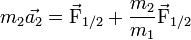
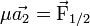
L'approximation de la masse nulle

Comme on l'a vu, pour deux corps isolés du reste de l'univers (c'est-à-dire qu'on considère que les forces appliquées sur les deux objets par le reste de l'univers sont négligeables), les deux objets sont en orbite elliptique admettant comme un de ses foyers le centre de masse de l'ensemble (dans un référentiel galiléen). Quand un des objets est bien plus lourd que l'autre, le mouvement de l'objet le plus lourd est imperceptible.

On fait donc l'approximation de supposer l'objet le plus lourd (1) fixe ; son centre de masse est un des foyers de la trajectoire elliptique de l'autre corps (2).

L'accélération du corps 1 est proportionnelle à la masse du corps 2, indépendante de la masse du corps 1, et inversement. En faisant tendre vers zéro la masse du corps 2, on trouve bien la fixité du corps 1.

On peut alors introduire le concept fictif de particule de masse infinitésimale, utilisée dans la définition de l'unité astronomique. En effet, la définition actuelle de cette unité implique une particule de masse infinitésimale, donc n'exerçant aucune force sur le Soleil.

Le concept d'un objet de masse réellement nulle pose un léger problème en mécanique newtonienne. En effet, l'accélération exercée par le Soleil sur un corps est indépendante de sa masse, et demeure la même lorsque cette masse tend vers zéro, puisque la force de gravitation est proportionnelle à la masse et l'accélération, inversement proportionnelle à la force. Dès lors, on peut se demander ce qui se passe quand la masse est nulle. Un premier raisonnement est de considérer que l'accélération reste la même, puisqu'elle ne change pas lorsque la masse tend vers zéro. Mais on peut objecter que la masse étant nulle, il n'y a aucune force de gravité entre les deux corps. Mais la force provoquant une accélération d'un corps de masse nulle est effectivement nulle, sans que l'accélération le soit nécessairement. Dans tous les cas, la force exercée sur le corps massif est nulle. Et dans tous les cas, la conservation de la quantité de mouvement est vérifiée.

Finalement, la mécanique newtonienne laissait irrésolue la question « quelle accélération subit un corps de masse nulle sous l'effet de la gravitation ? ». Cette question fut tranchée par la relativité générale, qui fait de la gravitation une courbure de l'espace-temps lui-même, et donc indique sans ambiguïté que les corps de masse nulle sont également accélérés par la gravité.