Proportionnalité - Définition

Quatrième proportionnelle

La quatrième proportionnelle est le quatrième nombre à mettre dans un tableau de proportionnalité dont 3 cases sont déjà remplies. Ce quatrième nombre s'obtient en faisant le produit des nombres situés sur une même diagonale et en divisant par le troisième nombre.

Cette technique est appelée "règle de trois" ou "produit en croix".

Exemple. On considère que le nombre de pages et proportionnel au nombre d'heures passées à les écrire. Il faut 6 heures pour écrire un rapport de 33 pages, combien d'heures faut-il pour un rapport de 55 pages ?

Tableau de proportionnalité:

Réponse :

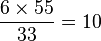
Quantités inversement proportionnelles

Deux quantités sont inversement proportionnelles , si l'une est proportionnelle à l'inverse de l'autre. Cette condition équivaut à ce que leur produit soit constant.

Exemple : pour parcourir 100 km, le temps est inversement proportionnel à la vitesse.

• à 100 km.h^-1, il faut 1 h
• à 50 km.h^-1, il faut 2 h
• à 10 km.h^-1, il faut 10 h

Leur produit est constant et représente la distance parcourue

• 100 km.h^-1 × 1 h = 50 km.h^-1 × 2 h = 10 km.h^-1 × 10 h = 100 km

Représentation graphique

Representation graphique de y=kx

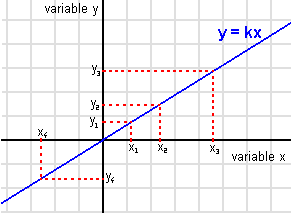
Dans un plan euclidien muni d'un repère cartésien, un point M est repéré par ses deux coordonnées x (l'abscisse) et y (l'ordonnée). Les coordonnées x=0 et y=0 correspondent à l'origine. Supposons que x et y représentent les valeurs de mesures (éventuellement dans une unité fixée si les grandeurs mesurées sont physiques). Soit une séquence finie de données (x₁,y₁), ... (x_n,y_n). Ces données peuvent être interprétées comme les coordonnées respectivement des points M₁,...,M_n. La grandeur ou variable y varie linéairement en fonction de la grandeur ou variable x si et seulement si les points O, M₁,...,M_n sont alignés. Autrement dit, tous les points M_i sont situés sur une même droite passant par l'origine. Cette droite D est tracée en bleu ci-contre. Par extrapolation, une nouvelle mesure donnerait un couple (x, y) qui correspondrait aux coordonnées d'un point de la droite D.

Il existe un réel k tel que tous les points de D sont exactement les points de coordonnées (x,kx). Autrement dit, un couple (x, y) correspond aux coordonnées d'un point de D si et seulement si y = k×x. Le réel k est appelé pente ou coefficient directeur de la droite. C'est aussi le coefficient de proportionnalité de y par rapport à x, On dit aussi que y ou y(x) est une fonction linéaire de x.

Lors d'une expérience, il se peut que des erreurs soient commises lors des relevés des mesures x et y. Les points O, M₁,...,M_n placés dans le graphique se retrouvent alors à proximité d'une droite, de pente k. Une certaine liberté de choix demeure sur la pente k, mais des choix en un sens meilleurs peuvent être faits, en utilisant des méthodes dites de régression linéaire.