Règle de trois - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
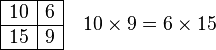
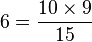
La règle de trois ou règle de proportionnalité est une méthode mathématique permettant de déterminer l'un des termes d'un tableau de proportionnalité à partir des autres. Elle peut aussi être utilisée pour vérifier qu'un tableau de valeurs satisfait une relation de proportionnalité.
Cette règle repose sur l'égalité des produits en croix, qui sont les produits des termes de chaque diagonale dans un tableau de proportionnalité à deux lignes et deux colonnes.
Elle se retrouve notamment dans le calcul de pourcentages, dans la résolution de problèmes de conversion d'unités, en application du théorème de Thalès ou encore dans la caractérisation de la colinéarité de deux vecteurs du plan à l'aide de leurs coordonnées.
| Algèbre |
| Logique |
| Arithmétique |
| Probabilités |
| Statistiques |
Explication
Le principe de la règle de trois consiste à se ramener à l'unité.
Par exemple, considérons la question :
- Si pour fabriquer 5 objets il faut 7 heures de travail, combien d'heures faut-il pour fabriquer 8 objets ?
- Déterminons le temps nécessaire à la production d'un objet :
En 7 heures, sont fabriqués 5 objets. Donc la fabrication d'un objet dure

- Nous pouvons donc en déduire le temps nécessaire à la production de 8 objets :
Si pour 1 objet il faut

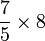
Le terme de Règle de trois provient du fait qu'elle fait intervenir 3 nombres (ici 5, 7, 8). La mise en place d'une règle de trois nécessite une rédaction rigoureuse pour placer ces trois nombres dans la fraction finale. Cette rédaction peut être avantageusement remplacée par un tableau de proportionnalité. De plus, l'utilisation d'un tel tableau permet d'utiliser l'égalité du produit en croix (égalité du produit des diagonales).
Soit x le temps de fabrication de 8 objets :
| nb objets | 5 | 1 | 8 |
| temps (en h) | 7 |
|
|
Ici, on passe de la deuxième colonne à la troisième colonne en divisant par 5, puis de la troisième colonne à la dernière colonne en multipliant par 8. Après avoir converti en minutes pour effectuer les calculs, on obtiendra le nombre manquant qui est donc: x = 11h12min.
Le tableau de proportionnalité permet de raccourcir encore le raisonnement en mécanisant le calcul. On peut trouver directement le résultat de cette façon :
| 5 | 8 |
| 7 |
|
Le résultat final s'obtient en effectuant le produit des deux termes d'une diagonale et en divisant par le terme restant.
-
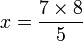
C'est sous cette forme qu'elle est maintenant présentée en France.
Extensions
Règle de trois inverse
Il y a des grandeurs qui diminuent à proportion d'un accroissement des données. Par exemple, si on demande en combien de temps 10 ouvriers construiront un certain mur que 15 ouvriers ont pu élever en 12 jours, on considèrera qu'il faut, pour construire un tel mur, un travail égal à
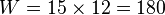
travail qui est, dans une large mesure, indépendant du nombre d'hommes ou du temps disponible, mais ne dépend que de la taille du mur. Ainsi, le temps recherché t doit être tel que :
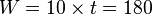
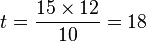
Règle de trois composée
On rencontre parfois des problèmes de proportion faisant intervenir deux « règles de trois » enchaînées, ou même plus. En voici un exemple :
18 ouvriers travaillant à raison de 8 heures par jour ont pavé en 10 jours une rue longue de 150 m. On demande combien il faut d'ouvriers travaillant 6 heures par jour pour paver en 15 jours une rue longue de 75 m, rue de même largeur que la précédente.
Lagrange propose la règle suivante : Si une quantité augmente en même temps, dans la proportion qu'une ou plusieurs autres quantités augmentent, et que d'autres quantités diminuent, c'est la même chose que si on disait que la quantité proposée augmente comme le produit des quantités qui augmentent en même temps, divisé par le produit de celles qui diminuent en même temps.
Dans l'exemple qu'on vient de donner, pour une même largeur de route,
- il faut plus d'ouvriers si la longueur de rue à paver augmente ;
- il faut moins d'ouvriers si la durée journalière de travail augmente ou si le nombre de jours accordé pour faire le travail augmente.
Donc le nombre N d'ouvriers cherché est donné par :