Récurrence transfinie - Définition

Introduction

La récurrence transfinie, appelée aussi sous l'influence anglaise induction transfinie, permet de construire des objets et de démontrer des théorèmes sur des ensembles infinis.

Elle généralise la récurrence ordinaire sur en considérant des familles indexées par un ordinal infini quelconque au lieu de se borner au plus petit d'entre eux qu'est , appelé ω en tant que nombre ordinal.

Une fois acquis le concept d'ordinal, on dispose là d'un outil très commode, que l'on peut utiliser conjointement avec l'axiome du choix à la place du lemme de Zorn, pour faire des constructions conformes à l'intuition et où l'on dispose de renseignements précis pour une étude approfondie.

Notions préliminaires

Comme nous parlerons beaucoup des ordinaux dans cet article il peut être pertinent de rappeler que les ordinaux sont des sortes de nombres, c’est-à-dire que le début de la classe des ordinaux (ceux plus petits que ω) peut être identifié à l'ensemble des nombres naturels, et que les relations donnant à sa structure (successeur, somme, produit ...) peuvent être étendues à la classe des ordinaux (avec quelques différences importantes, par exemple ).

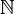
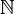
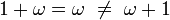
Démonstration par récurrence transfinie

• L'objectif est de démontrer qu'une certaine propriété vaut pour tout objet d'un domaine considéré.
• En arithmétique on dispose d'un schéma d'axiomes permettant de le faire sur l'ensemble des entiers, voir raisonnement par récurrence.
• En théorie des ensembles c'est un théorème applicable à toute classe bien ordonnée, les ordinaux étant les archétypes d'ensembles bien ordonnés.

Sur la classe des ordinaux

Une classe (propre) est un rassemblement d'ensembles qui ne peut sans contradiction être considérée comme un ensemble, comme la classe V de tous les ensembles. Voir classe. Les ordinaux forment une classe propre (c'est le paradoxe de Burali-Forti), car sinon leur type de bon ordre serait un ordinal plus grand que tous les ordinaux, ce qui est évidemment absurde.

Soit F(x) une formule avec pour seule variable libre x, on a alors :

• Théorème : (théorème *)

où On(α) signifie : α est un ordinal.

• La démonstration se fait de la manière suivante :

Supposons que : (prop. 1)

S'il existait un ordinal α tel que F(α) soit fausse, alors il en existerait un plus petit (la classe des ordinaux est elle-même bien ordonnée par la relation d'appartenance) ; soit α₀ cet ordinal. Pour tout ordinal β plus petit que lui, on aura donc F(β) ; ainsi est vrai (car F(β) est vrai ou et est faux). Et donc par hypothèse (prop.1) F(α₀) est vrai aussi ; contradiction.

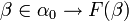
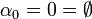
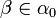
Cela montre que l'hypothèse qu'il existe un ordinal α tel qu'on n'ait pas F(α) est fausse ; par contraposition, il en découle que la prop.1 implique que pour tout ordinal γ, F(γ), ce qu'il fallait démontrer.

Sur un ensemble

On peut voir un ensemble comme une classe qui appartient à une autre classe.

Sur un ensemble bien ordonné

Voir aussi l'article : Ensemble bien ordonné

Un ensemble A muni d'une relation de bon ordre < est une structure (A, < ) où la relation binaire <

• est une relation d'ordre
• telle que tout sous ensemble non vide de A ait un et un seul plus petit élément pour < .

Théorème :

• soit B un sous ensemble de A (ordonné par l'ordre induit],
• si le plus petit élément de A est élément de B
• et si ,
• alors A = B.

Sur un ordinal

On restreint seulement le (théorème *) à un ordinal (ici Ord), ce qui donne :

Soit F(x) une formule avec pour seule variable libre x, et un ordinal Ord on a alors :

Utilisation du théorème

Nous nous restreindrons au cas de la classe des ordinaux :

il faut démontrer (prop. 1) à savoir F(α) en supposant F(β) pour tout β appartenant à α.

En général cette preuve se scinde en 3 cas selon que α est 1. l'ensemble vide 2. un ordinal successeur ou 3. un ordinal limite.

Qu'il faille aussi envisager le cas où α est un ordinal limite constitue la nouveauté dans les utilisations du principe de récurrence qui sont présentés dans l'article raisonnement par récurrence sur les seuls entiers.