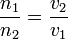Réfraction - Définition

Introduction

Le pinceau nous paraît brisé à cause de la réfraction de la lumière lorsque celle-ci traverse le dioptre eau-air.

Réfraction.

La réfraction, en physique des ondes — notamment en optique, acoustique et sismologie — est un phénomène de déviation d'une onde lorsque sa vitesse change entre deux milieux. La réfraction survient généralement à l'interface entre deux milieux, ou lors d'un changement de densité ou d'impédance du milieu.

On peut représenter une telle onde par deux approches :

• par son front d'onde : c'est la ligne que décrit une vague dans l'eau (optique ondulatoire et sismologie) ;
• par un rayon : c'est la direction de propagation de l'onde, perpendiculaire au front d'onde (optique géométrique).

Les deux modèles sont équivalents dans le cas de la réfraction, cependant on préfèrera le premier pour expliquer le phénomène, et le second pour le quantifier.

Description

Le crayon nous paraît brisé à cause de la réfraction de la lumière.

La lumière est déviée lorsqu'elle passe d'un milieu transparent à un autre (par exemple : de l'air à l'eau, ou le contraire…). C'est ce phénomène qu'on observe lorsque l'on regarde une paille dans un verre : celle-ci paraît brisée. Cette fracture apparente est à l'origine du mot réfraction.

La lumière est dite « réfractée » et la propriété qui caractérise les différents milieux transparents est la « réfringence », qui se traduit par une valeur numérique : l’ « indice de réfraction ».

Approche ondulatoire : Principe de Huygens-Fresnel

La célérité de la lumière n'est pas la même dans les deux milieux. Ce changement de valeur suffit à interpréter le changement de direction de l'onde. C'est Christian Huygens donne un modèle, en associant la propagation de la lumière à la propagation d'un front d'onde (1673) et l'utilisera pour expliquer la double réfraction du spath d'Islande, observée par Bartholin.

Le principe de Huygens-Fresnel

Le principe de Huygens-Fresnel stipule qu'à une interface, tous les points atteints par une onde venant d'un premier milieu réémettent une onde dans le second milieu. On peut alors interpréter la réfraction comme la déviation du front d'onde liée à la vitesse plus faible (ou plus rapide) de ces ondes réémises.

Huygens — s'opposant ainsi à Newton — considérait que la lumière était une onde, se propageant de proche en proche dans les milieux transparents. Il imaginait le front d'onde comme la superposition d'ondelettes, de sorte qu'au passage d'un dioptre, la célérité étant différente de part et d'autre, la taille des ondelettes était changée d'autant et le front dévié en conséquence. Le rapport des indices des milieux apparaît alors simplement comme le rapport des célérités :

On peut également utiliser ce même principe pour rendre compte de la réflexion (il suffit en effet de considérer la partie des ondelettes se déployant dans le premier milieu) et de la diffraction.

Construction de Huygens du rayon réfracté

Cette interprétation permet également une construction géométrique. Celle-ci est semblable à celle de Descartes, mais elle s'appuie sur la comparaison des célérités.

Les rayons à tracer sont alors en 1/n₁ et 1/n₂ et le raisonnement géométrique repose sur l'intersection commune des plans d'onde (point B), qui, par nature doivent être tangents aux ondelettes.

L'ondelette la plus grande correspond sur la figure à la position du front d'onde s'il n'y avait pas de dioptre (ici n₂ > n₁), tandis que le cercle le plus petit correspond donc au front de l'onde diffractée.

Le rayon réfracté est donc bien selon (IC) (I étant le point d'incidence).