Résistance des matériaux - Définition

Introduction

Essai de compression sur une éprouvette de béton, une pression croissante est appliquée verticalement sur l'échantillon pendant que deux appareils mesurent les déformations longitudinales et transversales de l'éprouvette

À l'issue du test, l'éprouvette s'est rompue. Notez la cassure longitudinale

La résistance des matériaux, aussi appelée RDM, est une discipline particulière de la mécanique des milieux continus permettant le calcul des contraintes et déformations dans les structures des différents matériaux (machines, génie mécanique, bâtiment et génie civil).

La RDM permet de ramener l'étude du comportement global d'une structure (relation entre sollicitations — forces ou couples — et déplacements) à celle du comportement local des matériaux la composant (relation entre contraintes et déformations). L'objectif est de concevoir la structure suivant des critères de résistance, de déformation admissible et de coût financier acceptable.

Lorsque l'intensité de la contrainte augmente, il y a d'abord déformation élastique (le matériau reprend sa forme initiale lorsque la sollicitation disparaît), puis déformation plastique (le matériaux ne reprend pas sa forme initiale lorsque la sollicitation disparaît, il subsiste une déformation résiduelle), et enfin rupture (la sollicitation dépasse la résistance intrinsèque du matériau).

Histoire

Premier cours de Résistance des Matériaux donné par August Wöhler à l'Université de Göttingen en 1842. (sources : voir discussion)

Notion de poutre

L'ingénieur utilise la résistance des matériaux avant tout pour déterminer les dimensions des éléments de construction et vérifier leur résistance et leur déformation. L'un des éléments structurels le plus fréquent est la poutre, c'est-à-dire un objet de grande longueur par rapport à sa section, chargée dans son plan moyen de symétrie.

Hypothèses de la RDM

Dans son utilisation courante, la RDM fait appel aux hypothèses suivantes :

Le matériau est :

• élastique (le matériau reprend sa forme initiale après un cycle chargement déchargement),
• linéaire (les déformations sont proportionnelles aux contraintes),
• homogène (le matériau est de même nature dans toute sa masse),
• isotrope (les propriétés du matériau sont identiques dans toutes les directions).

Le problème est :

• en petits déplacements (les déformations de la structure résultant de son chargement sont négligeables et n'affectent pratiquement pas sa géométrie),
• quasi-statique (pas d'effet dynamique),
• quasi-isotherme (pas de changement de température).

Principes fondamentaux de la théorie des poutres

Deux des dimensions de la poutre sont petites par rapport à la troisième. En d'autres termes les dimensions de la section droite sont petites par rapport à la longueur de la poutre. Ce principe permet d'approximer la poutre par une ligne (droite ou courbe) et des sections droites.

En général, une longueur ou une distance de l'ordre de deux à trois fois la plus grande dimension de la section droite est considérée suffisante pour appliquer le modèle RDM.

Le principe de Saint-Venant précise que le comportement en un point quelconque de la poutre, pourvu que ce point soit suffisamment éloigné des zones d'applications des forces et des liaisons, est indépendant de la façon dont sont appliquées les forces et de la façon dont sont physiquement réalisées les liaisons; le comportement dépend alors uniquement du torseur des forces internes en ce point.

La conséquence est que les contraintes produites par un système de forces dans une section éloignée du point d'application de ces forces ne dépendent que de la résultante générale et du moment résultat du système de forces appliquées à gauche de cette section.

Le modèle RDM n'est plus valide lorsque le principe de Saint Venant n'est pas satisfait, c'est-à-dire à proximité des liaisons, des appuis ou des points d'application des forces. Dans ces cas particuliers, il faut appliquer les principes de la Mécanique des milieux continus.

Le principe de Navier-Bernoulli précise que les sections droites le long de la fibre moyenne restent planes après déformation. Les déformations dues à l'effort tranchant montrent que les sections droites ne peuvent pas rester planes mais subissent un gauchissement. Pour tenir de ce fait l'énoncé de ce principe peut prendre la forme suivante: deux sections droites infiniment voisines deviennent après déformation deux sections gauches superposables par déplacement. Comme ce déplacement est petit, on peut considérer que les allongements ou raccourcissements de tout tronçon de fibre sont des fonctions linéaires des coordonnées de la fibre dans le plan de la section.

La loi de Hooke précise que, dans le domaine élastique du matériau, les déformations sont proportionnelles aux contraintes.

Le principe de superposition permet de décomposer toute sollicitation complexe en une somme de sollicitations élémentaires dont les effets sont ensuite additionnés. Ce principe est directement lié à l'hypothèse de linéarité de la loi de Hooke.

L'équilibre statique d'un système exige que :

• La somme des forces extérieures en tout point est égale au vecteur nul :

.

• La somme des moments calculés en tout point est égale au vecteur nul :

.

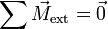
le théorème de Castigliano définit le déplacement du point, lieu d'application d'une force, par la dérivée du potentiel élastique par rapport de cette force.