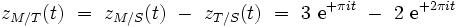Rétrogradation - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La rétrogradation ou mouvement rétrograde est un mouvement qui s'effectue dans le sens inverse du mouvement naturel lors de l'observation du mouvement apparent des planètes.
Premier mouvement
L'observation du mouvement des planètes se fait à partir de la Terre. Le premier mouvement apparent des planètes et des astres est dû à la rotation de la Terre autour d'elle-même. C'est un mouvement diurne qui s'effectue d'est en ouest, mouvement dont le Soleil est le premier exemple.
Exemple de la rétrogradation de Mars
Les données expérimentales réelles sont les suivantes :
| Distance moyenne au Soleil (en ua) | Période de révolution (en année terrestre) | Excentricité | Inclinaison (par rapport à l'écliptique) | |
|---|---|---|---|---|
| Terre | 1 | 1 | 0,016 710 22 | 0 |
| Mars | 1,5 | 1,88 | 0,093 412 33 | 1° 51' |
Approximation
Les excentricités des deux planètes étant faible (0,017 et 0,093) on peut assimiler les deux trajectoires elliptiques par des cercles (excentricité égale à 0). L'inclinaison de Mars étant petite, on peut assimiler en première approximation les deux trajectoires par des cercles coplanaires dont le centre est le Soleil.
Pour simplifier encore davantage, on va utiliser des données arrondies, et étudier le modèle simplifié suivant :
| Rayon du cercle (en demi ua) | Période de révolution (en année terrestre) | |
|---|---|---|
| Terre | 2 | 1 |
| Mars | 3 | 2 |
Avec ce modèle simplifié, les positions respectives de la Terre et de Mars (mesurées en demi unité astronomique) par rapport au Soleil peuvent être écrites en fonction du temps t (mesuré en année terrestre) comme des nombres complexes (i2 = − 1) :
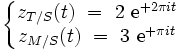
On en déduit que la position relative de Mars par rapport à la Terre est donnée par :
|
|
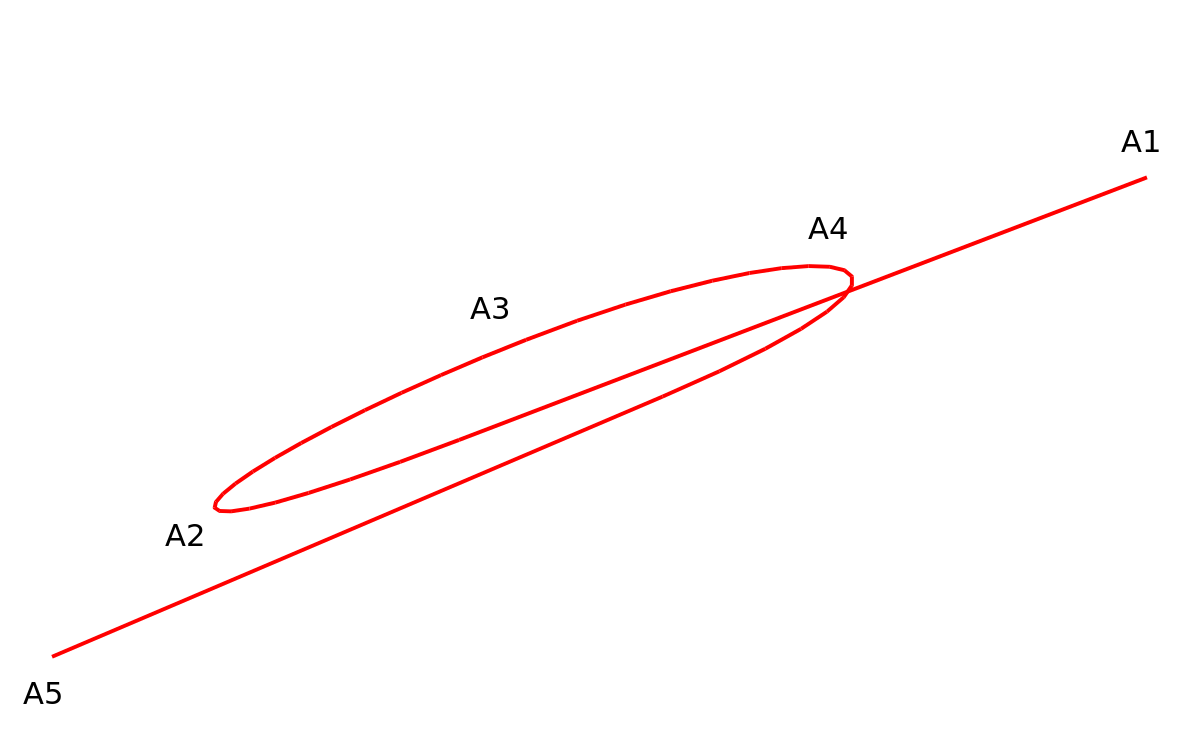
La représentation de cette position relative dans le plan donne la trajectoire suivante :
Second mouvement
Le deuxième mouvement est de l'ordre de l'année ou plus, et est dû aux mouvements de la Terre et des planètes autour du Soleil. Pour observer ce mouvement, il faut choisir un référentiel fixe. Ce sera l'ensemble des étoiles lointaines. Cet ensemble était appelé par les astronomes de l'antiquité jusqu'au XVIIIe siècle, la sphère des étoiles fixes. C'est donc par rapport aux étoiles fixes que ce mouvement apparent est mesuré. Observé à partir du Soleil, le mouvement apparent de chaque planète serait circulaire quasi-uniforme. Cependant, la source d'observation étant la Terre, le mouvement de la Terre introduit un biais dans l'observation et les planètes extérieures semblent alors parfois reculer dans leur mouvement. C'est ce qu'on appelle le mouvement rétrograde. Il s'explique par les différences relatives de vitesse angulaire de chaque mouvement.
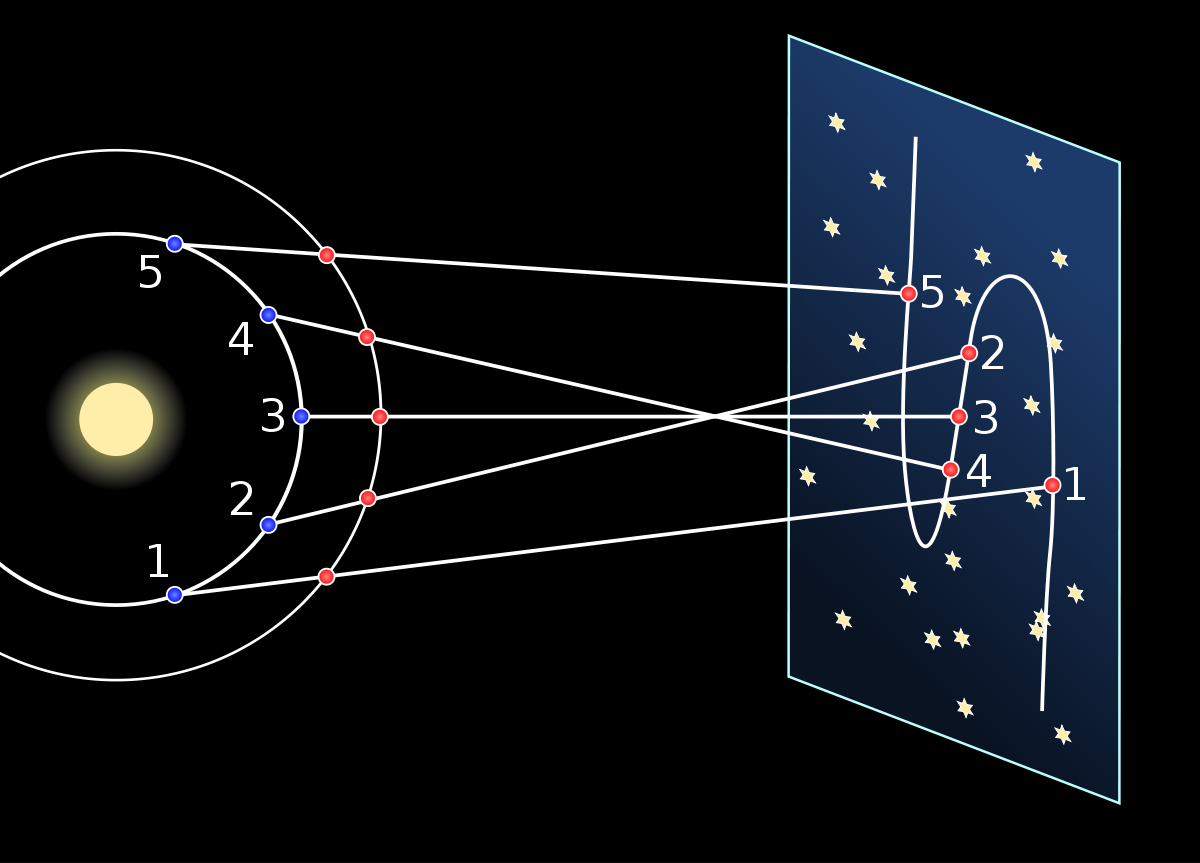
Explication du phénomène
Le dessin ci-contre schématise l'observation du mouvement d'une planète extérieure par projection sur la sphère des étoiles fixes. La Terre et la planète extérieure sont supposées évoluer sur des cercles (en réalité des ellipses de faible excentricité) dont le centre est le Soleil S. La Terre se déplace deux fois plus vite (en vitesse angulaire) que la planète observée. Les positions T1, T2, ..., T5 correspondent aux positions de la Terre et les positions P1, P2, …, P5 aux positions de la planète. Les mouvements apparents de la planète correspondent à la projection sur la sphère des étoiles fixes (considérablement rapprochée sur le schéma), c’est-à-dire aux points A1, A2, …, A5. La planète semble alors reculer dans son trajet A2, A3, A4.
L'existence d'un mouvement rétrograde a contraint les astronomes tenants du géocentrisme à imaginer des mouvements complexes des planètes pour expliquer ce phénomène, notamment l'épicycle.