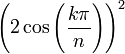Triangle de Pascal - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, le triangle de Pascal, est une présentation des coefficients binomiaux dans un triangle. À la ligne i et à la colonne j (0 ≤ j ≤ i) est placé le coefficient binomial
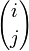
Il fut très tôt utilisé pour développer des expressions de la forme
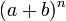
Histoire
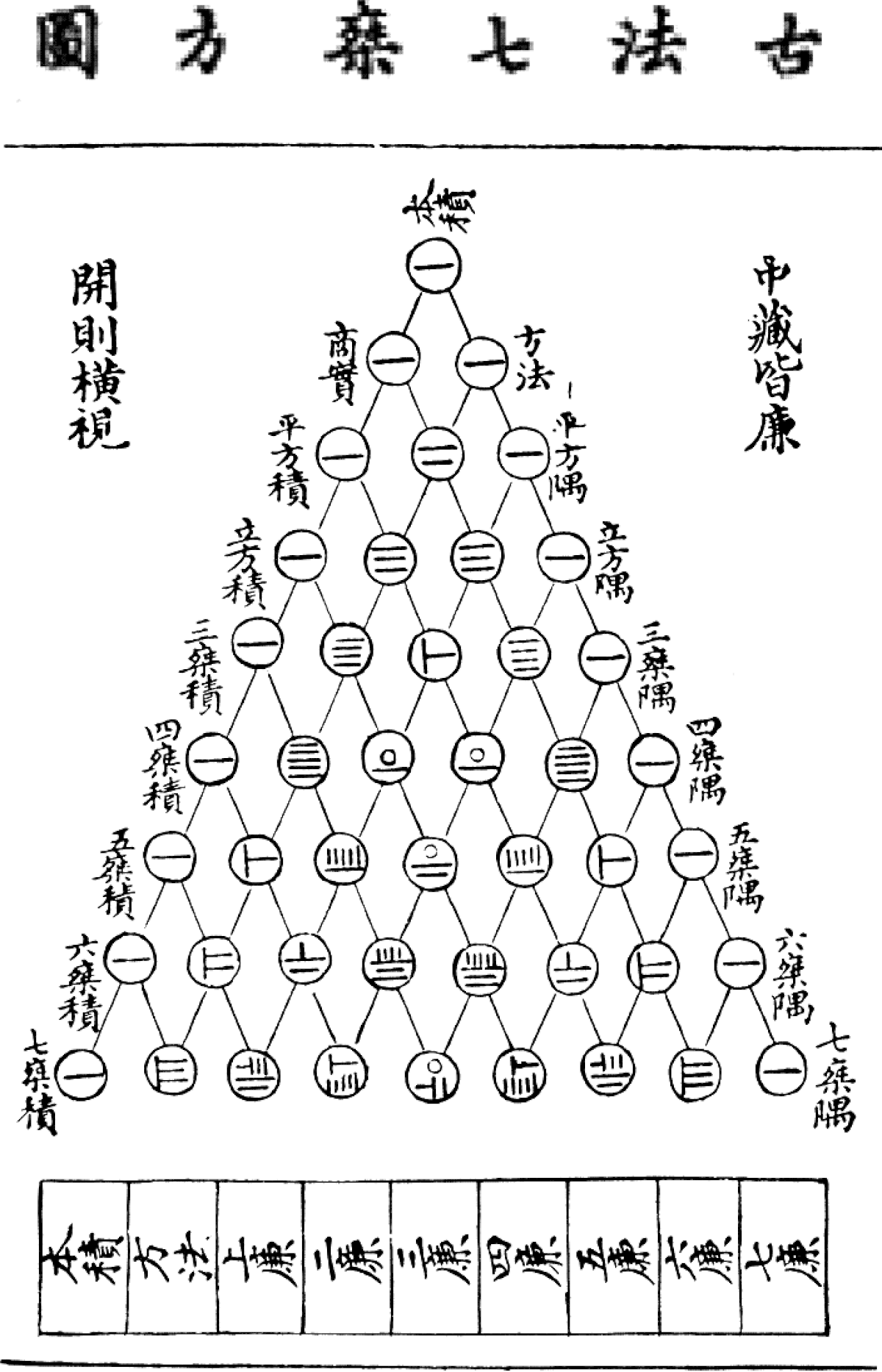
La tradition attribue le nom de triangle de Pascal au triangle décrit plus haut. Cependant, ce triangle était déjà connu en Orient et au Moyen-Orient plusieurs siècles avant la publication de Blaise Pascal. Il était ainsi connu des mathématiciens persans, par exemple al-Karaji (953 - 1029) ou Omar Khayyam au XIe siècle qui l'utilisent pour développer (a + b)n. Il apparaît en Chine dès 1261 dans un ouvrage de Yang Hui (au rang 6) et dans le Miroir de jade des quatre éléments de Zhu Shijie en 1303 (au rang 8). Yang Hui attribue la paternité du triangle au mathématicien chinois du XIe siècle Jia Xian. Ce triangle permettait de présenter les coefficients des différents termes dans la formule du binôme et, selon V. J. Katz, il était utilisé pour généraliser à des degrés supérieurs à deux la méthode d'extraction de racine.
En Europe, il apparait dans l'ouvrage de Peter Apian, Rechnung (1527). Il est étudié par Michael Stifel (1486 - 1567), Tartaglia (1499 - 1557) et François Viète (1540-1603). C'est d'ailleurs sous le nom de « triangle de Tartaglia » qu'il est connu en Italie. Mais c'est Blaise Pascal qui lui consacre un traité : le Traité du triangle arithmétique (1654) démontrant 19 de ses propriétés, propriétés découlant en partie de la définition combinatoire des coefficients. Nombre de ces propriétés étaient déjà connues mais admises et non démontrées. Pour les démontrer, Pascal met en place dans son traité une version aboutie du raisonnement par récurrence. Il y démontre le lien entre le triangle et la formule du binôme. Il l'utilise dans la résolution d'un problème de partage équitable des enjeux dans un jeu de hasard qui est interrompu avant le terme défini (problème des partis).
Propriétés
Liées à la construction
- La somme des termes d'une ligne : la somme des termes sur la ligne de rang n (première ligne = rang 0) est égale à 2n.
- Les crosses de hockey : Si on fait la somme des termes, en partant d'un bord du triangle et en descendant verticalement, on obtient le terme situé en diagonale en bas à droite du dernier terme de la colonne. Si on fait la somme des termes, en partant d'un bord du triangle et en descendant en diagonale vers la droite, on obtient le terme situé sous le dernier terme de la diagonale.
- Exemple : descente de 4 termes dans la colonne de rang 3 : 1 + 3 + 6 + 10 =.20 terme situé en bas à droite du dernier terme
- Exemple : Descente en diagonale de 5 termes à partir de la ligne de rang 4 : 1 + 5 + 15 + 35 + 70 = 126 terme situé sous le dernier
- Diagonale ascendante : la somme des termes d'une diagonale ascendante correspond à l'un des termes de la suite de Fibonacci
- Diagonales ascendantes de rang 1, 2, 3, 4, 5 : 1, 1, 1 + 1 = 2 , 1 + 2 = 3, 1 + 3 + 1 = 5
- Chaque ligne possède un centre de symétrie
Formule du binôme
Le triangle de Pascal est souvent utilisé dans les développements binomiaux. En effet, on trouve sur une même ligne tous les coefficents intervenant dans le développement d'une puissance de la somme de deux termes.
- Exemple :
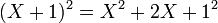
- Généralisation :
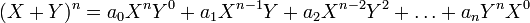
Connaissant ainsi la formule de sommation
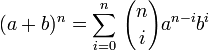
Posons a = b = 1, on a alors
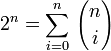
Posons a = 1 et b = -1, on a alors
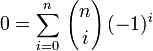
Connaissant ces deux égalités, dont l'une est une somme alternée, il vient que la somme des termes d'ordre 0, 2, 4,... dans une rangée est 2n − 1 et est égale à la somme des termes d'ordre 1, 3, 5, ....
Propriété liée au dénombrement
Le nombre situé dans la colonne p(en comptant à partir de 0 les colonnes) et la ligne n (en comptant à partir de 0 les lignes) indique le nombre de combinaisons possibles de p éléments dans un ensemble à n éléments.
Dans la ligne n et la colonne p, on a
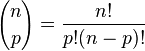
- Dans la ligne n et la colonne p, on lit le nombre de fois où l'on peut espérer obtenir p piles et n-p faces lors de 2n lancers d'une pièce équilibrée
- En multipliant un terme par le rang de sa colonne et en le divisant par le rang de sa ligne, on obtient le terme situé en cran plus haut sur la gauche
- exemple le terme dans la ligne 6 et la colonne 4 est 15 (on rappelle que les lignes et les colonnes sont numérotées en commençant à 0); Or 15 × 4/6=10 situé dans la case juste à côté en haut à gauche.
- En multipliant le terme de ligne n et de colonne p par
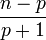
- Tous les termes de la ligne de rang n (sauf le premier et le dernier) sont multiples de n si et seulement si n est un nombre premier
Nombres de Catalan
Toutes les lignes de rang pair (2n) ont un terme central, en divisant ce terme par n+1 ou en lui ôtant son voisin, on obtient un nombre de Catalan.
Triangle de Sierpinski
En grisant les cases où apparaît un nombre impair et blanchissant les cases où apparaît un nombre pair, on obtient une image analogue au triangle de Sierpinski. Il en est de même si on noircit toutes les cases qui ne sont pas congrues à 0 modulo p.
Nombres figurés
Les nombres situés sur la troisième diagonale descendante correspondent aux nombres triangulaires, ceux de la quatrième diagonale aux nombres tétraédriques, ceux de la cinquième diagonale aux nombres pentatopiques et ceux de la n-ième diagonale aux nombres n-topiques.
Formules trigonométriques
La formule du binôme appliqué à la formule d'Euler (cos(θ) + isin(θ))n = cos(nθ) + isin(nθ) permet de développer cos(nθ) et sin(nθ).
Les coefficients situés sur la ligne de rang n permettent d'écrire tan(nθ) en fonction de t = tan(θ)
- Exemple : sur la ligne 4 on lit 1 - 4 - 6 - 4 - 1 et
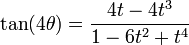
- Formule générale :
![\tan(n\theta) = \frac{\sum_{k=0}^{[(n-1)/2]}{(-1)^k {n \choose 2k+1}t^{2k+1}}}{\sum_{k=0}^{[n/2]}(-1)^k{n \choose 2k}t^{2k}}](https://static.techno-science.net/illustration/Definitions/autres/6/6202105ed210496af892ea36d5d92f6a_721b8f8a284a461d61f4993700840f34.png)
![\tan(n\theta) = \frac{\sum_{k=0}^{[(n-1)/2]}{(-1)^k {n \choose 2k+1}t^{2k+1}}}{\sum_{k=0}^{[n/2]}(-1)^k{n \choose 2k}t^{2k}}](https://static.techno-science.net/illustrationWebp/Definitions/autres/6/6202105ed210496af892ea36d5d92f6a_721b8f8a284a461d61f4993700840f34.png)
Les coefficients situés sur une diagonale ascendante permettent d'exprimer sin(n θ) comme produit de sin(θ) par un polynôme en cos(θ) (voir Polynôme de Tchebychev) :
- Exemple : sur la diagonale ascendante de rang 5, on lit 1 - 3 - 1 et
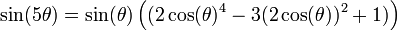
- Généralisation : si les termes de la diagonale ascendante de rang n sont
![a_{n,0}, a_{n,1}, \cdots a_{n,[(n-1)/2]}](https://static.techno-science.net/illustration/Definitions/autres/2/2c311e4802c919231671d758bfcb625e_c5fd2ebafac87238a0ffe93e26639f52.png)
![\sin(n\theta) = \sin(\theta)\left(\sum_{k=0}^{[(n-1)/2]}(-1)^k a_{n,k}\left(2\cos(\theta)\right)^{n-1-2k}\right)](https://static.techno-science.net/illustration/Definitions/autres/4/47eab2e413973e4f54ce38dfc4bfb166_4473485451a5a76a96a00d07005e3ed0.png)
![a_{n,0}, a_{n,1}, \cdots a_{n,[(n-1)/2]}](https://static.techno-science.net/illustrationWebp/Definitions/autres/2/2c311e4802c919231671d758bfcb625e_c5fd2ebafac87238a0ffe93e26639f52.png)
![\sin(n\theta) = \sin(\theta)\left(\sum_{k=0}^{[(n-1)/2]}(-1)^k a_{n,k}\left(2\cos(\theta)\right)^{n-1-2k}\right)](https://static.techno-science.net/illustrationWebp/Definitions/autres/4/47eab2e413973e4f54ce38dfc4bfb166_4473485451a5a76a96a00d07005e3ed0.png)
Par conséquent, les coefficients situés sur la diagonale ascendante de rang n permettent de déterminer un polynôme de degré [(n-1)/2] dont les racines sont les valeurs
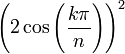
- Exemple : sur la diagonale de rang 7, on lit 1 - 5 - 6 - 1, on sait donc que les
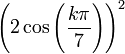
- Généralisation :
![P(x) = \sum_{k=0}^{[(n-1)/2]}(-1)^k a_{n,k} x^{[(n-1)/2] - k}](https://static.techno-science.net/illustration/Definitions/autres/4/4c6d521b40075234cbc0ee81df9e7a1e_34b087acd1c7ad776d6b0bb03905912f.png)
![P(x) = \sum_{k=0}^{[(n-1)/2]}(-1)^k a_{n,k} x^{[(n-1)/2] - k}](https://static.techno-science.net/illustrationWebp/Definitions/autres/4/4c6d521b40075234cbc0ee81df9e7a1e_34b087acd1c7ad776d6b0bb03905912f.png)
