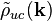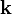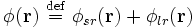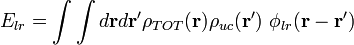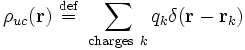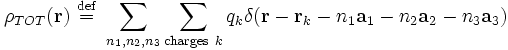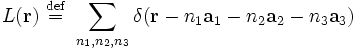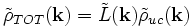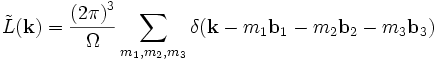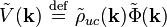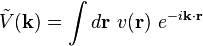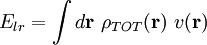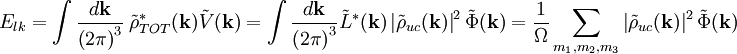Sommation d'Ewald - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La sommation d'Ewald (ou parfois somme d'Ewald) est une méthode de calcul des énergies d'interaction de systèmes périodiques (et particulier des cristaux), et tout particulièrement les énergies électrostatiques. La sommation d'Ewald est un cas particulier de la formule sommatoire de Poisson, avec le remplacement de la sommation des énergies d'interaction dans l'espace réel par une sommation équivalente dans un espace de Fourier. L'avantage de cette approche est la convergence rapide de la sommation dans l'espace de Fourier comparée à son équivalent dans l'espace réel lorsque les interactions se font à longue distance. Les énergies électrostatiques comprenant à la fois des termes d'interactions de courtes et de longues portées, il est très intéressant de décomposer le potentiel d'interaction en termes de courte portée - dont la sommation se fait dans l'espace réel - et de longue portée - dont la sommation se fait dans l'espace de Fourier.
La méthode fut développée par Paul Peter Ewald en 1921 (voir références) afin de déterminer l'énergie électrostatique (et, par là, la constante de Madelung) des cristaux ioniques.
Principe
La sommation d'Ewald réécrit le potentiel d'interaction comme la somme de deux termes :
où 
représente le terme de courte portée dont la sommation est rapide dans l'espace réel et 
le terme de longue portée dont la sommation est rapide dans l'espace de Fourier. La partie à longue portée doit être finie pour tous les arguments (en particulier pour r = 0) mais peuvent avoir une forme mathématique adéquate quelconque, le plus généralement une distribution gaussienne. La méthode postule que la partie à courte portée peut être sommée facilement, ainsi, le problème est de traiter la sommation du terme à longue portée. En raison de l'utilisation d'une intégrale de Fourier, la méthode postule implicitement que le système étudié est infiniment périodique (postulat pertinent pour un cristal parfait - i.e. pour l'intérieur d'un cristal réel). L'unité de base reproduite par périodicité est appelée maille unitaire. Une telle maille est choisie comme « maille centrale » de référence et les cellules reproduites par périodicité sont appelées images.
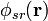
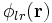
L'énergie d'interaction à longue portée est la somme des énergies d'interaction entre les charges d'une maille unitaire centrale et toutes les charges du réseau. Ainsi, elle peut être décrite comme une double intégrale deux champs de densités de charges correspondant aux champs de la maille unitaire et de celle du réseau cristallin.
où le champ de densité de charge de la maille unitaire 
est une intégration sur les positions 
des charges qk dans la maille unitaire centrale :
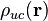
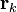
et le champ de densité de charge totale 
est la même intégration sur les charges de la maille unitaire qk et leurs images périodiques :
Ici, 
est la fonction δ de Dirac, 
, 
et 
sont les vecteurs de maille et n1, n2 et n3 sont des entiers. Le champ total peut être décrit comme une convolution de avec une fonction de réseau 
:
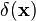
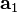
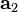
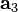
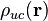
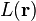
Puisque l'on a une convolution, la transformation de Fourier de est un produit :
dans laquelle la transformée de Fourier de la fonction de réseau est une autre intégration sur des fonctions δ :
où les vecteurs de l'espace réciproque sont définis comme il suit : 
(aux permutations cycliques près) où 
est le volume de la maille unitaire centrale (si c'est géométriquement un parallélépipède, ce qui est souvent mais pas nécessairement le cas). et 
sont des fonctions réelles paires.
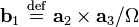
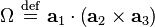
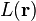
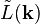
Pour la brièveté, on définit un potentiel effectif à une seule particule :
Cette équation étant aussi une convolution, la transformation de Fourier de cette équation est aussi un produit :
dans laquelle la transformée de Fourier est définié de la manière suivante :
L'énergie peut maintenant être écrite comme une intégrale d'un unique champ :
En utilisant le théorème de Parseval, l'énergie peut aussi être sommée dans l'espace de Fourier :
où 
dans la dernière intégrale.
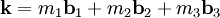
C'est le résultat principal. Une fois que 
est calculé, la sommation/intégration sur 
est simple et devrait rapidement converger. La raison la plus courante d'absence de convergence est une mauvaise définition de la maille unitaire, qui doit être électriquement neutre afin d'éviter des sommes infinies.