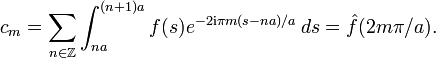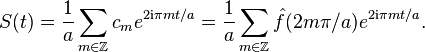Formule sommatoire de Poisson - Définition

Introduction

La formule sommatoire de Poisson (parfois appelée resommation de Poisson) est une identité entre deux sommes infinies, la première construite avec une fonction f, la seconde avec sa transformée de Fourier . Ici f est une fonction sur l'axe réel, ou plus généralement sur l'espace euclidien à n dimensions. La formule a été découverte par Siméon Denis Poisson.

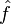
Elle, et ses généralisations, sont importantes dans plusieurs domaines des mathématiques, dont la théorie des nombres, l'analyse harmonique, et la géométrie riemannienne. L'une des façons d'interpréter la formule unidimensionnelle est d'y voir une relation entre le spectre de l'opérateur de Laplace-Beltrami sur le cercle et les longueurs des géodésiques périodiques sur cette courbe. La formule des traces de Selberg, à l'interface de tous les domaines cités plus haut et aussi de l'analyse fonctionnelle, établit une relation du même type, mais au caractère beaucoup plus profond, entre spectre du Laplacien et longueurs des géodésiques sur les surfaces à courbure constante négative (tandis que les formules de Poisson en n dimensions sont reliées au Laplacien et aux géodésiques périodiques des tores, espaces de courbure nulle).

Formule sommatoire de Poisson

Notations

Soit une fonction dont la transformée de Fourier est notée , c’est-à-dire :

, et .

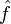
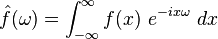
Théorème

Soit f une fonction complexe sur deux fois continûment différentiable ; on suppose que f et ses deux premières dérivées sur sont intégrables, et qu'elle satisfait l'estimation

Soit a un nombre strictement positif. Notons ω₀ = 2π / a, le mode fondamental, et la transformée de Fourier de f. Alors, on a l'identité suivante:

.

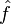
Démonstration de la formule

Le membre de gauche de la formule sommatoire de Poisson est la somme d'une série de fonctions continues. L'hypothèse faite sur le comportement de f à l'infini implique que cette série converge normalement sur tout compact [-a,a] de . Par conséquent, sa somme est une fonction continue, et la formule de définition montre qu'elle est périodique de période a.

Nous pouvons donc calculer les coefficients de sa série de Fourier en exponentielles complexes:

Du fait de la convergence normale de la série définissant S, on peut échanger intégration et sommation, et écrire ainsi

Si on effectue dans chaque intégrale le changement de variable t+na=s, on obtient

D'après nos hypothèses sur f et ses dérivées, et les identités classiques sur la transformée de Fourier d'une dérivée, on voit que la fonction vérifie l'estimation

.

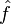
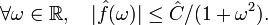
Par conséquent, la série des c_m est absolument convergente ; on est dans une situation où on peut sommer la série de Fourier de S, et on obtient

C'est la formule désirée, modulo le remplacement de 2π / a par ω₀.

Convention alternative

Si on utilise les conventions suivantes :

, ,

alors la formule sommatoire de Poisson se réécrit (avec et ) :

.

Sur les conditions de convergence

Une façon pratique de passer outre les conditions de régularité imposées à la fonction est de se placer dans le contexte plus général de la théorie des distributions. Si on note la distribution de Dirac alors si on introduit la distribution suivante :

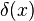
une façon élégante de reformuler la sommation est de dire que est sa propre transformée de Fourier.