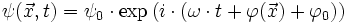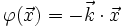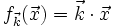Espace réciproque - Définition

Introduction

En physique, on utilise souvent des espaces abstraits pour caractériser les phénomènes, ce sont des espaces des phases.

Dans le cas des ondes, l'espace des phases est l'espace des vecteurs d'onde. Une onde plane et monochromatique est entièrement caractérisée par son vecteur d'onde. Or, la diffusion Rayleigh transforme une onde plane monochromatique en une somme d'ondes planes monochromatiques ; l'amplitude diffusée selon un vecteur d'onde donné est le produit de l'amplitude incidente ψ₀ par une fonction du vecteur d'onde  :

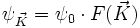
où F correspond à la transformée de Fourier 3D de l'objet diffractant l'onde (voir théorie de la diffraction sur un cristal).

Du point de vue mathématique, les vecteurs d'ondes ont la spécificité d'être les vecteurs propres des transformations linéaires, homogènes et continues (pouvant se formuler à l'aide d'un produit de convolution). La solution de nombreux problèmes physiques peut donc s'écrire comme une somme d'ondes planes monochromatiques.

Si les opérations sur les vecteurs d'onde n'ont pas de traduction simple dans l'espace réel (c'est une représentation dans l'espace des fréquences spatiales), ce qui va être intéressant, c'est la manière dont les propriétés de l'espace réel, et notamment les endroits où l'onde est diffusée, sont transposées dans cet espace des phases. L'espace des phases a alors une correspondance avec l'espace réel, on parle d'espace réciproque.

L'espace réciproque correspond à une représentation ondulatoire des objets (fréquentielle), duale de leur représentation corpusculaire (spatiale). Le célèbre principe d'incertitude de Heisenberg est l'expression physique du lien entre les deux représentations.

Un point remarquable est qu'un objet de type réseau cristallin est également un réseau du point de vue ondulatoire. On parle alors de réseau réciproque. L'espace réciproque est ainsi fréquemment utilisé en cristallographie et en physique du solide. Toutefois, pour en expliquer les concepts, nous allons présenter son application à des problèmes de diffraction en optique.

Le vecteur d'onde

La phase d'une onde varie en fonction du temps et de l'endroit considéré.

Pour simplifier, on prend φ₀ nul à l'origine O du repère. Le terme spatial s'exprime sous la forme d'un produit scalaire :

où est le vecteur reliant l'origine O (φ = 0) au point considéré. La norme de est 2π/λ (en rad·m^-1), λ étant la longueur d'onde.

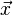
La « raison d'exister » du vecteur d'onde est le produit scalaire. Si l'on note la fonction :

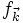
on voit que cette fonction est une forme linéaire ; l'ensemble de ces formes linéaires est un espace vectoriel isomorphe à l'espace des phases. De fait, l'espace des phases est un espace dual.

Physiquement, le vecteur d'onde correspond à une description ondulatoire d'un objet (onde plane monochromatique) alors que le vecteur position correspond à une description corpusculaire. Selon le principe d'incertitude de Heisenberg, les deux descriptions sont intimement liées et un objet réel ne peux qu'être approximativement décrit par l'une ou l'autre puisqu'il n'est ni monochromatique ni parfaitement localisé. Seule la fonction d'onde décrit complétement l'objet, et ce, quelle que soit la base utilisée (fréquentielle ou spatiale).

Conventions de notation pour l'article

Dans les exemples suivants, nous considérons que l'espace est muni d'une base orthonormée directe , ces vecteurs définissant respectivement les axes x, y et z.

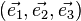
Le plan contenant les fentes d'Young, le réseau ou les lames de verre est le plan (y,z) ; l'axe des x est normal à ce plan.

Les composantes du vecteur sont notées K_x, K_y et K_z.