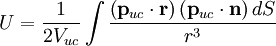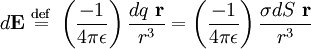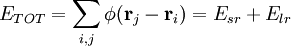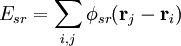Sommation d'Ewald - Définition

Terme dipolaire

L'énergie électrostatique d'un cristal polaire (c'est-à-dire un cristal avec un dipôle identifié dans la maille unitaire) est semi-convergente, i.e. elle dépend de l'ordre de la sommation. Par exemple, si les interactions dipôle-dipôle d'une maille unitaire centrale avec des mailles unitaires sont localisées sur un cube toujours croissant, l'énergie converge vers une valeur différente de celle obtenue pour une intégration sphérique. En d'autres termes, cette semi-convergence se produit car : premièrement, le nombre de dipôles interagissants dans une couche de rayon R augmente en R² ; deuxièmement, la force d'une interaction dipôle-dipôle simple décroît en  ; et troisièmement, la sommation mathématique diverge.
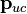
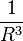
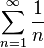
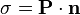
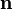
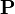
Ce résultat relativement surprenant peut être concilié avec le fait que l'énergie des cristaux réels est finie car ceux-ci ne sont pas infinis, et donc des limites particulières. Plus spécifiquement, la frontière d'un cristal polaire montre une densité de charge effective surfacique sur sa surface où est le vecteur normal à la surface et représente le moment dipolaire net volumique. L'énergie d'interaction du dipôle dans une maille unitaire centrale avec cette densité de charge surfacique peut être écrite :

où et V_uc sont les moments dipolaires nets et le volume de la maille unitaire, dS une aire infinitésimale sur la surface du cristal et est le vecteur de la maille unitaire à cette aire infinitésimale. Cette formule provient de l'intégration de l'énergie où représente le champ électrique infinitésimale généré par une charge surfacique infinitésimale (loi de Coulomb) :

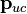
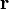
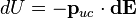
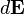
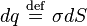
Le signe négatif provient de la définition de , qui pointe vers la charge, et non de la charge.

Méthode du maillage particulier d'Ewald

La sommation d'Ewald fut developpée comme méthode de physique théorique, bien avant la venue des ordinateurs et de l'informatique. Cependant, elle s'est très largement répandue depuis les années 1970 dans les simulations numériques de systèmes de particules, et tout particulièrement celles interagissant par des lois de forces en carré inverse, comme la gravité ou l'électrostatique. Les applications de ces simulations comprennent des objets aussi divers que les plasmas, les galaxies ou les biomolécules.
Comme dans une sommation d'Ewald « normale », un potentiel d'interaction générique est séparé en deux termes : - un terme d'interaction à courte portée à intégration rapide dans l'espace réel est un terme d'interaction à longue portée qui s'intègre rapidement dans l'espace de Fourier. L'idée de base de la sommation sur un maillage particulier d'Ewald est de remplacer la sommation directe des énergies d'interaction entre les particules ponctuelles :

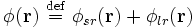
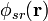
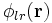
avec deux sommations, une intégration directe E_sr du potentiel à courte portée dans l'espace réel :

(partie particulière du maillage particulier d'Ewald) et une intégration dans l'espace de Fourier de la partie à longue portée :

où et représentent les transformées de Fourier du potentiel électrique et la densité de charge (partie Ewald). En raison de leurs convergences rapides dans leurs espaces respectifs (réel et de Fourier), elles peuvent être tronquées sans perte réelle de précision et un gain important du temps de calcul requis. Afin d'évaluer efficacement la transformée de Fourier du champ de densité de charge, on peut utiliser la transformée de Fourier rapide, qui nécessite que le champ de densité soit évaluée sur une maille discrète de l'espace (partie maillage).
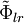
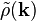
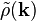
En raison du postulat de périodicité implicite de la sommation d'Ewald, les applications de la méthode du maillage particulier d'Ewald (particular mesh Ewald en anglais, abrégé par l'acronyme PME) aux systèmes physiques nécessitent d'imposer une symétrie par périodicité. Pour cette raison, la méthode est bien plus efficace pour les systèmes pouvant être simulé comme étant infinis dans l'espace. Dans les simulations de dynamique moléculaire, cette configuration est normalement atteinte en construisant de manière délibérée une maille unitaire de charge neutre qui peut être infiniment reproduite par pavage afin de former des images; cependant, afin de prendre correctement en compte les effets de cette approximation, ces images sont réincorporées dans la boîte de simulation originale. L'effet global est similaire à une version tridimensionnelle du jeu Asteroids, dans laquelle chaque dimension se « replie » sur elle-même. Cette propriété de la maille est appelée condition périodique aux limites. Afin de mieux visualiser cela, on peut imaginer un cube unitaire ; la face du dessus est en contact avec la face du dessois, la face de droite avec celle de gauche, et celle de devant avec celle de derrière. Il en résulte que la taille de la boîte doit être choisie avec précaution pour éviter de générer des corrélations de mouvement impropres entre deux faces « en contact », mais également assez petite pour pouvoir être traitée numériquement. La définition du rayon de coupure, distance à laquelle on passe de la partie d'interaction à courte distance de la partie interaction à longue distance, peut aussi introduire des artéfacts.
La restriction du champ de densité à un maillage rend la méthode PME encore plus efficace pour des systèmes avec des variations de densité « douces », ou des fonctions de potentiels continues. Les systèmes localisés (par exemple des systèmes radicalaires) ou avec de fortes variations de densité pourront être traités plus efficacement par la méthode des multipôles rapides de Greengard et Rokhlin.