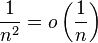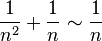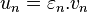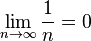Suite (mathématiques) - Définition

Remarque

L'usage (fréquent dans les articles de cette encyclopédie) du mot séquence est une mauvaise traduction de l'anglais sequence. La bonne traduction est suite.

Suites particulières

Suites de Cauchy

Dans ce paragraphe, on supposera que est un espace métrique.

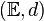
Une suite est dite de Cauchy lorsque : , tels que : , , et

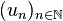
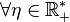
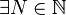
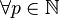
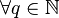
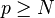
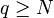
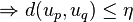
On démontre que

• Toute suite convergente est une suite de Cauchy.
• Toute suite de Cauchy est bornée.

On appelle espace complet un espace où toute suite de Cauchy est convergente.

Suites extraites

Soit une suite à valeurs dans un espace .

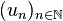
Si est une fonction strictement croissante (une telle fonction s'appelle une extractrice), on dit que la suite est une suite extraite (ou sous-suite) de la suite .

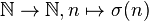
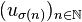
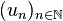
Grosso modo, c'est la suite pour laquelle on n'a gardé que certains termes (une infinité quand même).

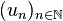
Ces suites extraites se révèlent intéressantes quand on cherche à déterminer des valeurs d'adhérence.

Suites équivalentes et suites négligeables

Définition

Soient et deux suites à valeurs réelles. et sont équivalentes si et seulement si

• telle que
• tel que

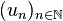
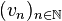
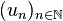
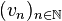
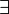
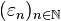
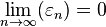
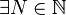
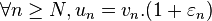
On note alors

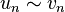
Remarque Si à partir d'un certain rang, alors si et seulement si

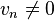
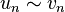
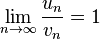
Définition

Soient et deux suites à valeurs réelles. On dit que est négligeable devant si et seulement si :

• telle que et , ce qu'on note u_n = o(v_n)

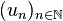
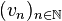
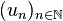
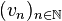
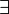
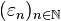
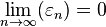
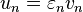
Remarque Si à partir d'un certain rang, alors u_n = o(v_n) si et seulement si

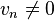
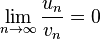
Exemple

Considérons et
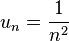
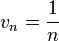
Posons On a alors :

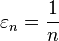
D'où et