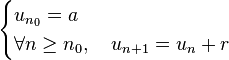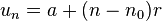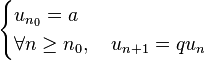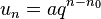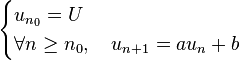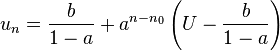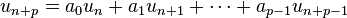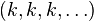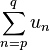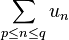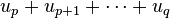Suite (mathématiques) - Définition

Exemples de suites

Suite arithmétique

C'est une suite à valeurs dans un groupe additif, définie par récurrence par

où r est une constante. Son terme général est alors

Suite géométrique

C'est une suite à valeurs dans un monoïde, définie par récurrence par

Où q est une constante. Son terme général est alors

Suites arithmético-géométriques

C'est une suite à valeurs dans un corps, définie par récurrence par

• Si a = 1, la suite est arithmétique
• Si , son terme général est alors

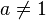
Suites récurrentes linéaires à coefficients constants

Une suite récurrente linéaire est définie par une relation de récurrence :

où a₀, a₁, …a_{p − 1} sont p scalaires (a₀ non nul). L’entier p est appelé l’ordre de la récurrence. Les suites à récurrence linéaire d’ordre 1 sont les suites géométriques ; une suite récurrente linéaire d’ordre 2 célèbre est la suite de Fibonacci. L’étude des suites récurrentes linéaires d’ordre p fait appel à la notion d’espace vectoriel et au calcul matriciel, et on dispose de méthodes permettant le calcul du terme général de n'importe quelle suite de ce type.

Quelques suites célèbres

Il est assez surprenant que ce soit dans l'univers des suites d'entiers que l'on trouve les suites les plus célèbres :

• la suite de Fibonacci où chaque terme est la somme des deux termes qui le précèdent et dont on connaît le terme général et sa relation avec le nombre d'or
• la suite de Conway, piège de test de QI, où chaque terme est la description à voix haute du terme précédent
• la suite de Syracuse ou de Collatz définie par une relation de récurrence simple : le terme suivant est obtenu en prenant, ou bien la moitié du terme précédent si celui-ci est pair, ou bien le triple du terme précédent augmenté de un si celui-ci est impair. Le comportement de cette suite reste encore une énigme pour les mathématiciens.

Notations

Soit A une partie de . Soit une suite d'éléments de E. Nous notons u_n l'image u(n) de l'entier n par u.

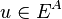
Ainsi, les images de sont notées .

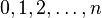
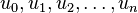
On dit que u_n est le terme de rang n, ou d'indice n de la suite u.

Nous notons en général la suite u : qui est donc une application.

Lorsque , nous notons plus simplement la suite : .

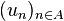
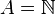
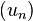
Lorsque , nous pouvons noter la suite ou encore .

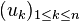
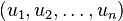
L'ensemble des suites d'éléments de E indexées par une partie A de se note ou E^A.

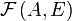
Remarque

Nous ne devons pas confondre la suite avec l'ensemble des valeurs de la suite qui est l'image directe de par u. Par exemple, considérons la suite , l'ensemble des valeurs de la suite est { − 1,1}.

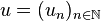
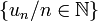
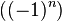
Exemples

La suite nulle est la suite dont tous les termes sont nuls :

.

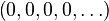
Plus généralement, si (u_n) est une suite et que , alors on dit que (u_n) est une suite « presque nulle », ou « nulle à partir d'un certain rang », ou encore « cofinale à zéro ».

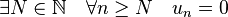
Pour des raisons de commodité, pour tout élément k de E on peut identifier k et la suite :

Posons ; est la suite des inverses des nombres entiers. Celle-ci peut être représentée par:

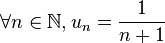
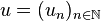
Terme général et récurrence

Une suite étant une application de A (partie de ) dans E , il est intéressant, voire primordial, de connaître l'image de n pour tout n de A. Si u_n est donné comme expression de n et permet un calcul direct du nombre, on dit que l'on connait le terme général de u_n.

Cependant, si , la nature de l'ensemble de départ permet de définir la suite par une relation de récurrence : le terme d'indice n est donné comme fonction de n et des termes d'indices k, k ≤ n. La propriété de récurrence permet d'affirmer qu'il suffit alors de donner pour en déduire tous les termes. En pratique, la détermination de va nécessiter le calcul de tous les termes de à , soit une opération bien longue. En programmation, cette récurrence a donné lieu à la création des fonctions récursives. Une partie de la recherche sur les suites va consister à déterminer le terme général d'une suite connaissant sa relation de récurrence.

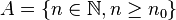
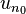
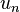
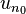
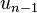
Exemple : la suite définie par u₀ = 1 et, pour tout entier n, u_{n + 1} = (n + 1)u_n est la suite des factorielles : u_n = n!

Somme des termes d'une suite

Si E est un groupe additif, on note :

ou

la somme :

Voir aussi : Série (mathématiques).