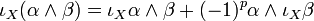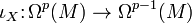Produit intérieur - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
En géométrie différentielle, le produit intérieur est une opération élémentaire sur les formes différentielles, que l'on construit à partir d'un champ de vecteur. Plus précisément, si X est un champ de vecteur sur une variété différentielle M, alors
est l'opérateur défini par
-
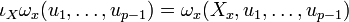
C'est une antidérivation de l'algèbre extérieure, i.e, si α est une p-forme et β une forme de degré quelconque :
-