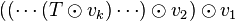Tenseur (mathématiques) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Principe général - Tenseurs et produit tensoriel sur les éléments - Produit tensoriel d'espaces vectoriels de dimensions finies - Permutation d'indices - Opération de contraction - Cas des espaces (pseudo)-euclidiens - Algèbre des tenseurs - Calcul pratique

Opération de contraction

Définition

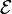
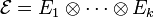
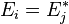
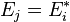
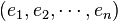
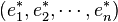
Soit $\mathcal{E}$ un espace vectoriel de dimension finie sur un corps $\mathbb{K}$ tel que $\mathcal{E} = E_1 \otimes \cdots \otimes E_k$ . On suppose qu'il existe deux indices $i$ et $j$ tels que $E_i = E_j^*$ (ou de manière complétement équivalente $E_j = E_i^*$ ). Soit $(e_1, e_2, \cdots, e_n)$ une base de $E i$ ; la base duale $(e_1^*, e_2^*, \cdots, e_n^*)$ est donc une base de $E j$ . 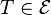Etant donné un tenseur $T \in \mathcal{E}$ , l'application

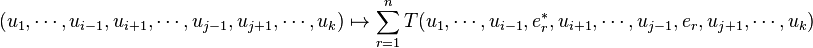
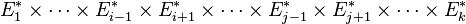
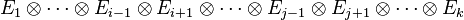
est une forme $(k - 2)$ -linéaire sur $E_1^* \times \cdots \times E_{i-1}^* \times E_{i+1}^* \times \cdots \times E_{j-1}^* \times E_{j+1}^* \times \cdots \times E_k^*$ , autrement dit un tenseur de $E_1 \otimes \cdots \otimes E_{i-1} \otimes E_{i+1} \otimes \cdots \otimes E_{j-1} \otimes E_{j+1} \otimes \cdots \otimes E_k$ . Par ailleurs cette forme est indépendante du choix de la base de $E i$ . L'opération s'appelle contraction de $T$ sur les indices $i$ et $j$ . Elle est parfois notée $tr i j$

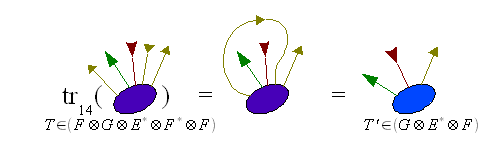
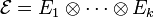
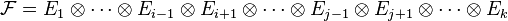
Il est important de garder à l'esprit que l'opération de contraction n'est possible que pour deux indices correspondant à des espaces duaux entre eux et n'a aucun sens dans d'autres cas. Il s'agit en outre d'une opération linéaire de $\mathcal{E} = E_1 \otimes \cdots \otimes E_k$ dans $\mathcal{F} = E_1 \otimes \cdots \otimes E_{i-1} \otimes E_{i+1} \otimes \cdots \otimes E_{j-1} \otimes E_{j+1} \otimes \cdots \otimes E_k$ .

Produit contracté

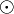
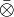
En pratique la contraction est souvent utilisée au sein d'un opération appelée produit contracté et notée $\odot$ , $\bar\otimes$ ou même simplement $\cdot$ . Le produit contracté de deux tenseurs est le résultat de leur produit tensoriel suivi d'une contraction d'un indice du premier par un indice du second. On notera que les notations sont lacunaires : elles ne précisent pas quels sont les indices de contraction. Par défaut, il s'agit en général du dernier indice du premier tenseur et du premier indice du second. Comme pour la contraction, le produit contracté ne fait sens que si les indices contractés correspondent à des espaces duaux.

Propriétés du produit contacté

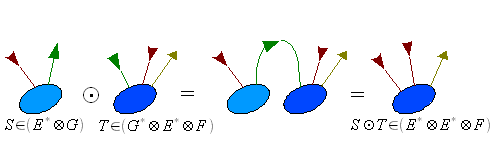
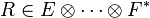
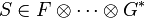
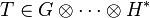
Associativité: Le produit contracté est associatif si le tenseur du centre a au moins deux indices. Ainsi pour $R \in E \otimes \cdots \otimes F^*$ , $S \in F \otimes \cdots \otimes G^*$ et $T \in G \otimes \cdots \otimes H^*$ , on a bien $(R \odot S) \odot T = R \odot (S \odot T)$ . Si le tenseur du centre n'a qu'un indice, il est possible que l'un des deux parenthésages ne fassent pas sens, et même dans le cas contraire, l'égalité ne sera pas réalisée dans le cas général.

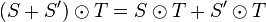
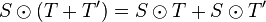
Distributivité: Le produit contracté se comporte bien comme un produit vis-à-vis de l'addition des espaces vectoriels :; $(S + S') \odot T = S \odot T + S' \odot T$; $S \odot (T+T') = S \odot T + S \odot T'$

Image par le tenseur ou produit contracté

Étant donné un tenseur

k

vecteurs tels que

on peut effectuer deux opérations :

calculer l'image des $k$ vecteurs par $T$ (qui, rappelons-le, peut toujours être vue comme une forme multilinéaire) : $T(v_1, \cdots, v_k)$ ;
calculer les produits contractés successifs de $T$ par chaque vecteur $((\cdots(T \odot v_k) \cdots ) \odot v_2 ) \odot v_1$ .

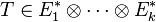
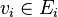
Il s'agit en fait d'une seule et même opération :

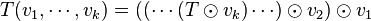
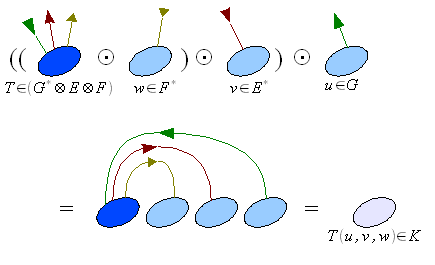
D'une manière plus générale, si

le tenseur

construit en évaluant la

i

-ème position de

T

est égal au produit contracté de

T

en son

i

-ème indice par

u

en son unique indice. Dés lors il devient possible d'occulter complétement l'aspect fonctionnel de

T

pour ne considérer que ses propriétés algébriques.

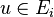
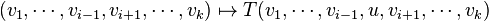
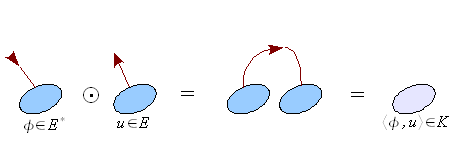
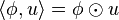
Crochet de dualité: Le crochet de dualité est donc un cas particulier du produit contracté : $\langle \phi, u \rangle = \phi \odot u$ .

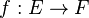
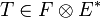
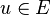
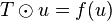
Image par une application linéaire: L'application linéaire $f : E \rightarrow F$ pouvant être vue comme un tenseur de $T \in F \otimes E^*$ , on peut calculer l'image d'un vecteur $u \in E$ comme étant le produit contracté $T \odot u = f(u)$ .

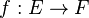
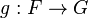
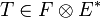
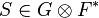
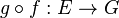
Composée d'applications linéaires: Si $f : E \rightarrow F$ et $g : F \rightarrow G$ sont représentées par les tenseurs $T \in F \otimes E^*$ et $S \in G \otimes F^*$ , alors l'application composée $g \circ f : E \rightarrow G$ peut être représentée par le tenseur $S \odot T$ .

Produit contracté plusieurs fois

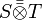
La contraction peut être exercée plusieurs fois à la suite d'un produit tensoriel. Par exemple le produit doublement contracté (noté $:$ , $\bar\bar\otimes$ ou par deux points dans un cercle) correspond à deux contractions successives après un produit tensoriel. Là encore les indices de contractions n'étant en général pas précisés, le produit doublement contracté $S \bar\bar\otimes T$ correspond souvent à la contraction du dernier indice de $S$ par le premier de $T$ et de l'avant dernier de $S$ par le deuxième de $T$ .

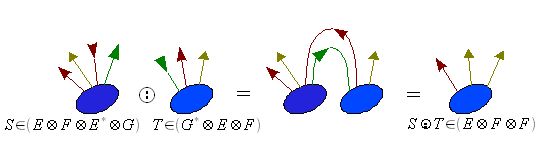
On peut définir de même un produit $n$ fois contracté si les tenseurs le permettent.

Permutation d'indices

Cas des espaces (pseudo)-euclidiens

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Existe-t-il des mélodies naturelles ? 🎶

Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

Page générée en 0.119 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise