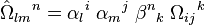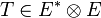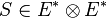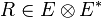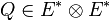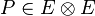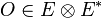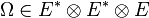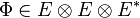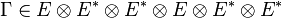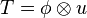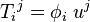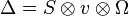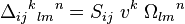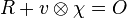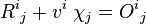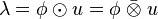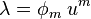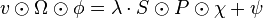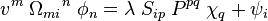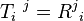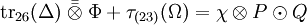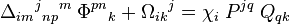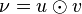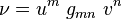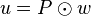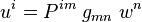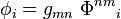Tenseur (mathématiques) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Principe général - Tenseurs et produit tensoriel sur les éléments - Produit tensoriel d'espaces vectoriels de dimensions finies - Permutation d'indices - Opération de contraction - Cas des espaces (pseudo)-euclidiens - Algèbre des tenseurs - Calcul pratique

Calcul pratique

La manipulation effective des tenseurs nécessite généralement de les représenter dans des bases particulières (mais néanmoins arbitraires).

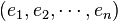
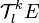
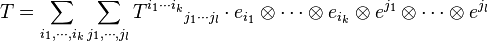
Soit $(e_1, e_2, \cdots, e_n)$ une base de $E$ . On notera $(e 1, e 2,... e n)$ sa base duale. 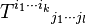Alors tout tenseur $T$ de $\mathcal{T}^k_l E$ peut s'écrire comme une combinaison linéaire de type : $T = \sum_{i_1,\cdots,i_k} \sum_{j_1,\cdots,j_l} T^{i_1\cdots i_k}{}_{j_1\cdots j_l} \cdot e_{i_1} \otimes \cdots \otimes e_{i_k} \otimes e^{j_1} \otimes \cdots \otimes e^{j_l}$ Si la base est précisée par avance la donne des scalaires $T^{i_1 \cdots i_k}{}_{j_1 \cdots j_l}$ caractérise entièrement le tenseur. Ils représentent les coordonnées du tenseur $T$ dans la base considérée. L'ensemble des conventions d'utilisation des coordonnées des tenseurs est appelé convention d'Einstein.

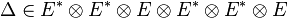
Il est possible de mélanger indices covariants et contravariants. Les indices contravariants sont notés en indices supérieurs, les indices covariants en indices inférieurs. Ainsi $\Delta \in E^* \otimes E^* \otimes E \otimes E^* \otimes E^* \otimes E$ se décompose dans une base donnée avec les composants $Δ i j k l m n$ .

Liens entre les notations

On se donne les tenseurs suivant :

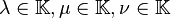
Scalaires : $\lambda \in \mathbb{K}, \mu \in \mathbb{K}, \nu \in \mathbb{K}$
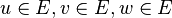
Vecteurs : $u \in E, v \in E, w \in E$
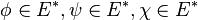
Covecteurs (formes linéaires) : $\phi \in E^*, \psi \in E^*, \chi \in E^*$
Tenseurs d'ordre 2 :

$T \in E^* \otimes E$
$S \in E^* \otimes E^*$
$R \in E \otimes E^*$
$Q \in E^* \otimes E^*$
$P \in E \otimes E$
$O \in E \otimes E^*$

Tenseurs d'ordre 3 et plus :

$\Omega \in E^* \otimes E^* \otimes E$
$\Phi \in E \otimes E \otimes E^*$
$\Delta \in E^* \otimes E^* \otimes E \otimes E^* \otimes E^* \otimes E$
$\Gamma \in E \otimes E^* \otimes E^* \otimes E \otimes E^* \otimes E^*$

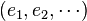
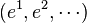
On choisit par ailleurs une base $(e_1, e_2, \cdots )$ dans $E$ . Ce choix induit naturellement celui de la base duale $(e^1, e^2, \cdots )$ dans $E *$ . Les tenseurs précédemment définis admettent alors une seule décomposition dans ces bases.

Notation des opérations dans les espaces de dimension finie
Propriétés	Notation standard	Convention d'Einstein
Produit tensoriel	$T = \phi \otimes u$	$T_i{}^j = \phi_i \; u^j$
	$\Delta = S \otimes v \otimes \Omega$	$\Delta_{ij}{}^k{}_{lm}{}^n = S_{ij} \; v^k \; \Omega_{lm}{}^n$
	$R + v \otimes \chi = O$	$R^i{}_j + v^i \; \chi_j = O^i{}_j$
Produit contracté	$\lambda = \phi \odot u = \phi \; \bar\otimes \; u$	$\lambda = \phi_m \; u^m$
Produit contracté	$v \odot \Omega \odot \phi = \lambda \cdot S \odot P \odot \chi + \psi$	$v^m \; \Omega_{mi}{}^n \; \phi_n = \lambda \; S_{ip} \; P^{pq} \; \chi_q + \psi_i$
Contraction	$μ = tr 12 (T)$	$μ = T m m$
Contraction	$tr 13 (Φ) = w$	$Φ m i m = w i$
Permutation d'indices	$T = τ (12) (R) = t R$	$T_i{\;}^j = R^j{}_i$
Permutation d'indices	$Γ = τ (123)(46) (Δ)$	$Γ i j k l m n = Δ j k i n m l$
Mélange	$\mathrm{tr}_{26}(\Delta) \; \bar\bar\otimes \; \Phi + \tau_{(23)}(\Omega) = \chi \otimes P \odot Q$	$\Delta_{im}{}^j{}_{np}{}^m \; \Phi^{pn}{}_k + \Omega_{ik}{}^j = \chi_i \; P^{jq} \; Q_{qk}$

Liens entre les notations dans le cas (pseudo-)euclidien

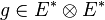
On considère par ailleurs l'existence du (pseudo-)produit scalaire $g \in E^* \otimes E^*$ .

Notation des opérations dans les espaces euclidiens
Propriétés	Notation standard	Convention d'Einstein
Produit contracté	$\nu = u \odot v$	$\nu = u^m \; g_{mn} \; v^n$
Produit contracté	$u = P \odot w$	$u^i = P^{im} \; g_{mn} \; w^n$
Contraction	$φ = tr 12 (Φ)$	$\phi_i = g_{mn} \; \Phi^{nm}{}_i$

A propos des changements de base

On notera que seule la convention d'Einstein admet des formules de changement de base. En effet, puisqu'elle prend le parti de représenter un tenseur par un jeu de coordonnées dans une base (voire plusieurs bases) prédéfinie, il existe des formules pour déterminer les coordonnées d'un même tenseur dans une nouvelle base ( comme $\hat{\Omega}_{lm}{}^n = \alpha_l{}^i \; \alpha_m{}^j \; \beta^n{}_k \; \Omega_{ij}{}^k$ ). La notation standard étant par définition indépendante d'un choix de base, elle n'admet pas d'équivalents pour ces formules.

Algèbre des tenseurs

Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋

Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️

Des singularités temporelles dans l'Univers ? 🕰️

Des fossiles de dinosaures mieux datés 🦖

Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭

Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆

Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜

Le rôle méconnu de la décharge dans l'usure des batteries 🔋

La fonte des glaces déplace les pôles: quelles conséquences ? 🌍

L'appareil photo de votre smartphone peut détecter l'antimatière 📱

Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐

Un mosasaure géant découvert dans le Mississippi 🦕

Problème, les galaxies meurent plus tôt que prévu 🌀

Ce lien entre cannabis et troubles psychotiques 🧠

Une révolution dans le refroidissement des puces électroniques ? 🔥

Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀

Lucy survole un astéroïde en forme de cacahuète 🚀

Découverte du fossile d'un dinosaure géant méconnu 🦕

Mars avait-elle un champ magnétique unilatéral ? 🔍

Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇

Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁

L'électroluminescence du graphène, une découverte inattendue ! 💡

Cet objet métallique n'a pas été fabriqué sur Terre 🔧

Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡

Cette super-Terre brûle les attentes des astronomes 🔥

Découverte exceptionnelle de fossiles d'amphibiens géants 🐸

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Page générée en 0.144 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise