Tenseur (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
sur les tenseurs
Tenseur
Tenseur (mathématiques)
Produit tensoriel
... de deux modules
... de deux applications linéaires
Algèbre tensorielle
Champ tensoriel
Espace tensoriel
Convention d'Einstein
Tenseur métrique
Tenseur énergie-impulsion
Tenseur de Riemann
... de Ricci
... d'Einstein
... de Weyl
... de Levi-Civita
... de Killing
... de Killing-Yano
... de Bel-Robinson
... de Cotton-York
Tenseur électromagnétique
Tenseur des contraintes
Tenseur des déformations
Modules
Algèbre extérieure
Les tenseurs sont des objets mathématiques issus de l'algèbre multilinéaire permettant de généraliser les scalaires et les vecteurs. On les rencontre notamment en analyse vectorielle et en géométrie différentielle fréquemment utilisés au sein de champs de tenseurs.
Le présent article ne se consacre qu'aux tenseurs dans des espaces vectoriels de dimension finie, bien que des généralisations en dimension infinie et même pour des modules existent.
Principe général
Le principe est de généraliser les notions de scalaires et de vecteurs de dimensions finies. Les tenseurs d'un type donné se comportent eux-mêmes comme des vecteurs :
- ils possèdent une addition et un produit par les scalaires ;
- ils sont indépendants d'un choix de bases mais peuvent être représentés par des tableaux à plusieurs entrées pour un choix de bases donnée.
À ceci s'ajoute deux opérations : un produit, dit tensoriel, permettant de multiplier deux tenseurs (éventuellement de natures distinctes) ainsi qu'une application linéaire qui réduit leur taille appelée contraction.
Comme évoqué ci-dessus les scalaires et les vecteurs constituent des exemples simples de tenseurs. Dans une base donnée un vecteur (tenseur d'ordre 1) peut être représenté par la donne d'un n-uplet de coordonnées. Les matrices
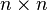
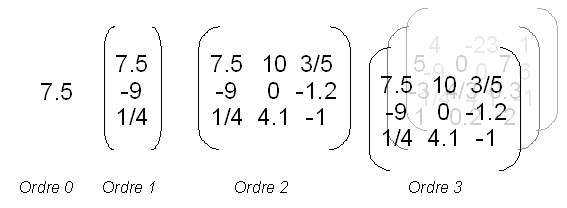
Les deux opérations classiques de la manipulation des tenseurs peuvent être intuitivement illustrés par certaines opérations matricielles. Il est en effet connu qu'en multipliant une matrice colonne par une matrice ligne (c'est-à-dire deux n-uplets) on obtient une matrice carrée (ou rectangulaire si les opérandes n'ont pas la même dimension). Il existe donc des transformations permettant d'augmenter l'ordre des tenseurs. Cette idée est à la base du produit tensoriel.
À l'inverse, le produit d'une matrice ligne par une matrice colonne se réduit à un scalaire. On voit ici apparaître l'idée de contraction.
Tenseurs et produit tensoriel sur les éléments
L'intérêt premier du produit tensoriel est de définir une opération sur les vecteurs (ou plus généralement les éléments des modules) ayant des propriétés similaires à celle d'un produit. Cela dit, contrairement aux produits habituels, le produit tensoriel n'est pas une opération interne : il peut s'effectuer sur des vecteurs issus d'espaces vectoriels différents et son résultat (à quelques exceptions prés) n'appartient à aucun des espaces en question. Les éléments intervenant dans de tels produits portent le nom de tenseurs.
Définition
Soit
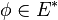
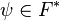
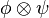
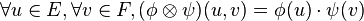
Il s'agit d'une forme bilinéaire : on a donc
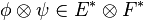
Comme en dimension finie E = E * * , tout vecteur u (respectivement v) peut être assimilé à une forme linéaire sur E * (respectivement F * ). On définit ainsi de manière générale le produit tensoriel de u et v, noté
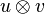
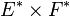
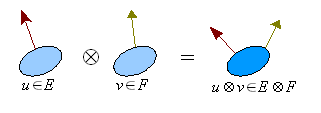
La forme bilinéraire
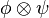
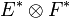
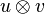
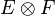
Remarques
- Réciproquement, tout tenseur
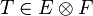
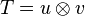
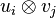
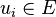
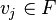
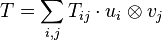
- On note bien que tout vecteur est un type de tenseur particulier (il est toujours assimilable à une forme 1-linéaire) et que tout tenseur fait partie d'un espace vectoriel. L'utilisation du terme tenseur sous-entend l'usage du produit tensoriel. En pratique le terme tenseur est surtout utilisé à propos de produits de vecteurs d'un même espace E ou de son dual E * .
Propriétés du produit tensoriel
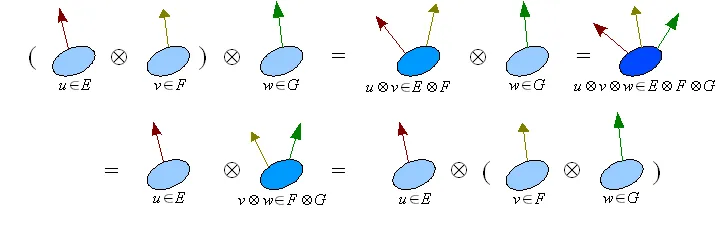
- Associativité
- Grâce à l'isomorphisme canonique on peut considérer que le produit tensoriel est associatif. Autrement dit
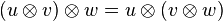
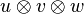
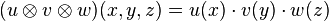
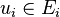
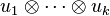
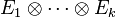
-
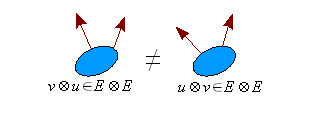
- Non commutativité
- Si
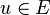
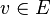
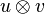
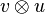
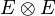
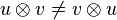
-
- Distributivité
- Le produit tensoriel se comporte bien comme un produit vis à vis de l'addition des espaces vectoriels :
-
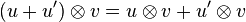
-
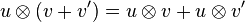
- Généralisation des produits usuels
- On notera que le produit tensoriel généralise le produit par un scalaire défini sur les
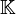
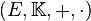
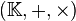
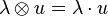
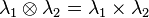
-

- Bases des espaces produits
- Soit
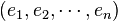
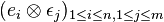
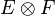
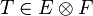
-
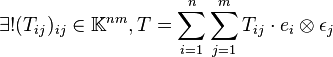
- Cette formule est bien cohérente avec le fait que
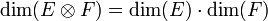
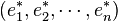
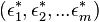
-
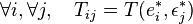
- Ces formules se généralisent pour k espaces vectoriels.