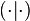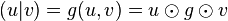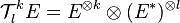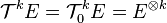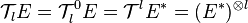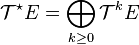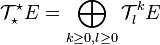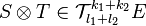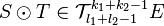Tenseur (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Cas des espaces (pseudo)-euclidiens
Dans un espace euclidien (ou pseudo-euclidien) E, l'existence d'un produit scalaire réel g (respectivement d'un pseudo-produit scalaire ; c'est-à-dire d'une forme bilinéaire symétrique non dégénérée) fournit des propriétés particulières aux tenseurs. Celui-ci permet en effet d'établir un isomorphisme canonique
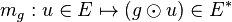
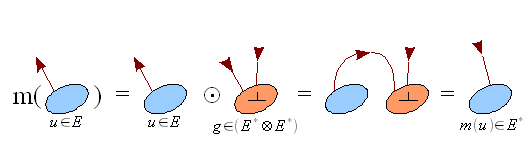
Le (pseudo-)produit scalaire sur E définit en outre naturellement un (pseudo-)produit scalaire sur E * . Il s'agit de l'unique élément de
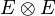
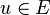
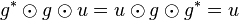
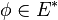
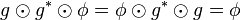
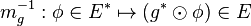
Assimilation avec le dual
Via l'isomorphisme mg on peut alors assimiler tout élément de E * à un élément de E :
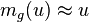
Propriétés
- Correspondance entre produits scalaire et contracté
- Il devient possible de contracter deux vecteurs de E. Cette contraction s'identifie au produit scalaire :
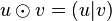
-
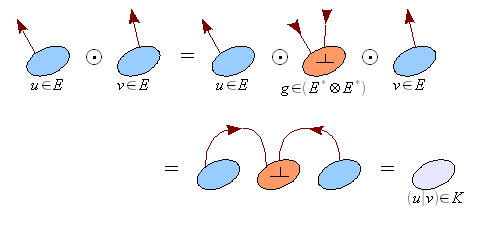
- Contractions sur des indices quelconques
- On peut maintenant contracter deux indices correspondant au même espace (pseudo-)euclidien E par utilisation implicite du produit scalaire :
-
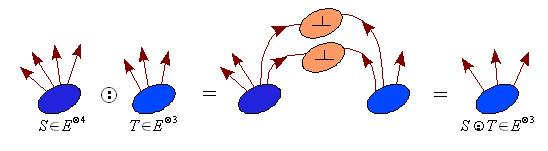
- A propos des espaces hermitiens
- Un produit scalaire hermitien n'est pas un tenseur : il n'est en effet que semi-linéaire par rapport à sa première variable. De fait, les propriétés énoncées ci-dessus ne s'appliquent pas dans le cadre des espaces hermitiens.
Algèbre des tenseurs
Définition
Etant donné un espace vectoriel de dimension finie E on appelle tenseur sur E k fois contravariant et l fois covariant (ou tenseur (k,l)) tout élément de
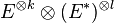
L'algèbre des tenseurs de E notée
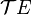
Les algébres
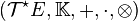
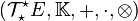
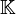

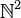
L'algèbre extérieure sur E notée ΛE possède des liens privilégiés avec l'algèbre
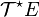
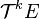
Elements
- L'algèbre tensorielle est surtout définie afin de donner une structure générale à l'ensemble des tenseurs. Ceci necessite de prolonger l'addition qui n'est a priori pas définie entre les éléments de
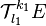
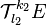
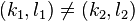
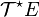
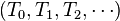
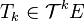
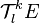
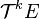
- Les éléments de
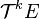
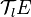
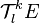
- En toute rigueur, l'algèbre
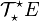
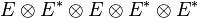
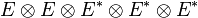
-
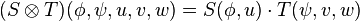
- Cette permutation permet d'affirmer que le produit tensoriel est bien une opération interne à
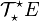
Propriétés
- Ordre
- Si S et T sont des tenseurs respectivement (k1,l1) et (k2,l2) sur E, alors
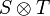
-
- Un produit contracté

-
- Trace des endomorphismes
- Un endomorphisme de E peut être vue comme un élément
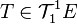
- Symétrie et antisymétrie
- Soit un tenseur T de
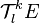
- On dit que T est symétrique par rapport aux indices i et j si τ(ij)T = T .
- On dit que T est antisymétrique par rapport aux indices i et j si τ(ij)T = − T .
- On dit que T est totalement symétrique s'il est symétrique pour tout couple d'indice. Il faut donc pour cela qu'il appartienne à
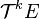
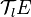
- On dit que T est totalement antisymétrique s'il est antisymétrique pour tout couple d'indice. Là encore, l'espace doit être
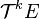
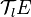
- Produit scalaire
- Un produit scalaire réel