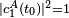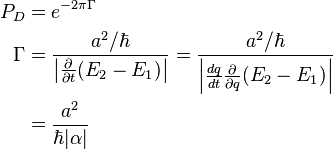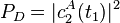Théorème adiabatique - Définition

Calcul des probabilités de passage diabatique

Formule de Landau-Zener

En 1932, une solution analytique au problème du calcul des probabilités de transition diabatique fut publié séparément par Lev Landau et Clarence Zener, pour le cas spécifique de la perturbation changeant linéairement dans laquelle la composante dépendant du temps n'est pas couplée aux états pertinents (par conséquent le couplage dans la matrice hamiltonienne diabatique est indépendant du temps).

Le principal apport de cette approche est la vélocité de Landau-Zener :

,

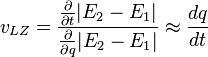
où est la variable de perturbation (champ magnétique ou électrique, longueur de liaison moléculaire, ou toute autre perturbation du système), et et sont les énergies des deux états diabatiques (se croisant). Une grande implique une grande probabilité de transition diabatique et inversement.

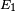
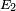
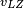
Si l'on utilise la formule de Landau-Zener, la probabilité d'une transition diabatique est donnée par :

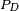
Approche numérique

Pour une transition impliquant une modification non linéaire de la variable de perturbation ou du couplage dépendant du temps entre les états diabatiques, les équations cinétiques de la dynamique du système ne sont pas analytiquement solvables. La probabilité de transition diabatique peut toujours être obtenue en utilisant une grande variété de algorithmes de résolution numérique des équations différentielles ordinaires.
Les équations à résoudre peuvent être obtenues à partir de l'équation de Schrödinger dépendante du temps :

,

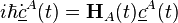
où est un vecteur contenant les amplitudes de l'état adiabatique, est le hamiltonien adiabatique dépendant du temps et le point supérieur indique une dérivée temporelle.

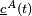
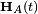
Une comparaison des conditions initiales utilisées avec les valeurs des amplitudes de l'état selon la transition peut indiquer la probabilité de transition diabatique. On a en particulier, pour un système à deux états :

si le système est initialisé avec .