Théorème adiabatique - Définition

Introduction

Le théorème adiabatique est un concept important en mécanique quantique. Sa forme originelle, énoncée en 1928 par Max Born et Vladimir Fock, peut être énoncée de la manière suivante :

Un système physique est maintenu dans son état propre instantané si une perturbation donnée agit sur lui suffisamment lentement et si il y a un intervalle significatif entre la valeur propre et le reste du spectre du hamiltonien.

Il peut ne pas être immédiatement compris à partir de cette formulation que le théorème adiabatique est, en fait, un concept extrêmement intuitif. Formulé simplement, un système quantique soumis à des conditions externes de modification graduelle peut adapter sa forme fonctionnelle, alors que dans le cas de modifications rapides, l'adaptation n'a pas le temps de se produire et par conséquent la densité de probabilité reste inchangée.
Les conséquences de ce résultat simple en apparence sont nombreuses, variées et extrêmement subtiles. On commence cet article par une description qualitative, suivie par quelques exemples, avant d'entamer une analyse rigoureuse. Enfin seront présentées quelques techniques utilisées pour les calculs d'adiabaticité.

Processus diabatiques et adiabatiques

Définitions quantiques

Un processus diabatique est un processus dans lequel les conditions (externes) changeant rapidement empêchent le système d'adapter sa configuration durant son déroulement, ce qui fait que la densité de probabilité reste inchangée. Typiquement, il n'y a pas d'état propre du hamiltonien final de même forme fonctionnelle que pour l'état initial. Le système finit en une combinaison linéaire d'états dont la somme reproduit la densité de probabilité initiale.
Un processus adiabatique est un processus dans lequel les conditions (externes) permettent l'adaptation du système, ce qui résulte en une modification de la densité de probabilité. Si le système est initialement dans un état propre du hamiltonien de départ, il sera au final dans l'état propre « correspondant » du hamiltonien d'arrivée.

Différentiation théorique

Pour un temps initial un système quantique a une énergie donnée par le hamiltonien  ; le système est dans un état propre de décrit par . Les conditions changeantes modifient le hamiltonien de manière continue, ce qui donne un hamiltonien final à un temps . Le système évolue selon l'équation de Schrödinger, afin d'atteindre l'état final . Le théorème adiabatique indique que la modification du système dépend de manière critique du temps durant lequel elle a lieu.
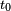
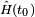
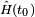
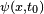
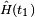
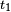
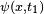
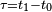
Pour un processus adiabatique véritable, on utilise  ; dans ce cas, l'état final est un état propre du hamiltonien final , avec une configuration modifiée :

.

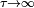
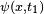
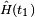
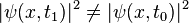
Le degré auquel un changement donné approche un processus adiabatique dépend à la fois de la séparation énergétique entre et les états adjacents, et la rapport entre l'intervalle à l'échelle de temps caractéristique de l'évolution de pour un hamiltonien indépendant du temps, , où est l'énergie de .

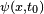
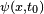
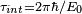
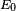
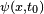
Inversement, dans la limite on a un passage infiniment rapide, ou diabatique ; la configuration de l'état reste inchangé :

.

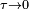
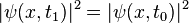
La condition dite « de gap » incluse dans la définition originale de Born et Fock donnée plus haut se réfère à la condition que le spectre de soit discret et non dégénéré, c'est-à-dire qu'il n'existe pas d'ambigüité dans l'ordre des états (on peut facilement établir quel état propre de correspond à ). En 1990, J.E. Avron et A. Elgart reformulèrent le théorème adiabatique, éliminant la condition de gap.
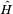
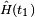
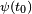
Le terme adiabatique est traditionnellement utilisé en thermodynamique afin de décrire des processus sans échange de chaleur entre le système et son environnement (voir adiabaticité). La définition quantique est plus proche du concept thermodynamique de transformation quasi-statique, et n'a pas de relation directe avec l'échange de chaleur. Ces deux définitions différentes peuvent être sources de confusion, particulièrement lorsque les deux concepts (échange de chaleur et processus suffisamment lents) sont présents dans un problème spécifique.