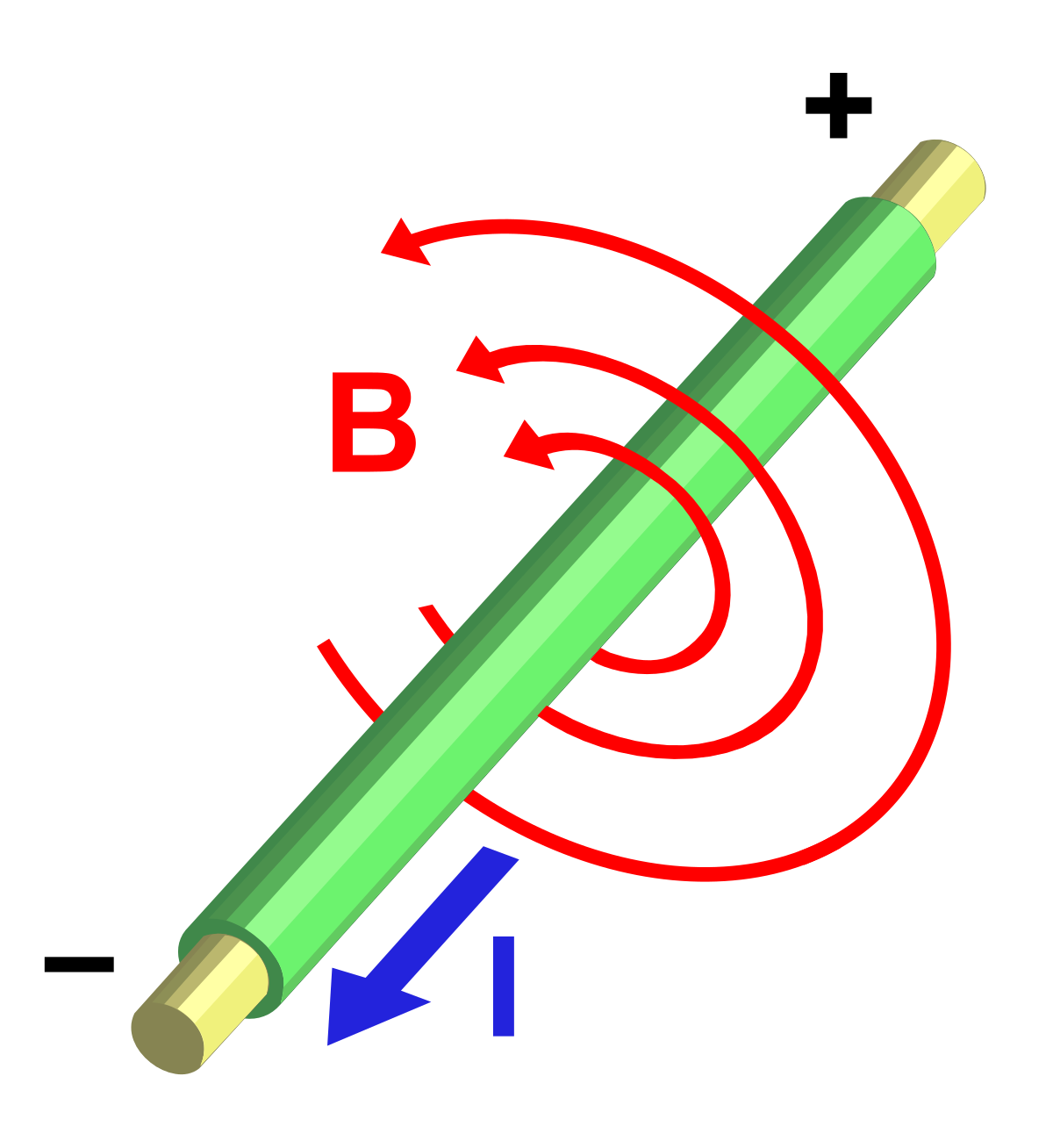
Théorème d'Ampère - Définition

Introduction

En magnétostatique le théorème d'Ampère permet de déterminer la valeur du champ magnétique grâce à la donnée des courants électriques. Ce théorème est une forme intégrale de l'équation de Maxwell-Ampère. Il a été découvert par André-Marie Ampère, et constitue l'équivalent magnétostatique du théorème de Gauss. Pour être appliqué analytiquement de manière simple, le théorème d'Ampère nécessite que le problème envisagé soit de symétrie élevée.

Énoncé du théorème d'Ampère

Un courant électrique I produit un champ d'induction électromagnétique B.

En régime quasi-permanent ou permanent, dans le vide, le théorème d'Ampère énonce que "la circulation, le long d'un circuit fermé, du champ magnétique engendré par une distribution de courant est égale à la somme algébrique des courants qui traversent la surface définie par le circuit orienté, multipliée par la perméabilité du vide (μ₀ = 4π.10 ^{− 7}H / m)."

où :

• représente l'intégrale curviligne sur le contour fermé τ,
• est l' induction magnétique,
• est l'élément infinitésimal de déplacement le long du contour τ,
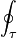
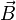
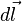
• μ₀ est la perméabilité du vide,
• est la somme algébrique des intensités des courants enlacés par le contour τ.

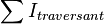
Par le théorème de Stokes, on obtient l'expression de la loi d'Ampère sous forme locale qui établit une relation entre le champ en un point de l'espace et la densité de courant en ce même point

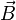
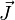
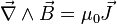
Lien avec les équations de Maxwell

L'équation de Maxwell-Ampère est la forme locale du théorème d'Ampère.

Intensité enlacée

On peut distinguer plusieurs cas concernant l'intensité enlacée par le circuit.

• si le circuit enlace un courant volumique j, alors l'intensité enlacée aura la forme suivante :
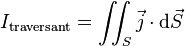
• si le circuit enlace plusieurs circuits filiformes alors on peut dire que l'intensité enlacée s'écrira : avec I_i l'intensité d'un fil du circuit filiforme.

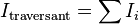
Attention, il s'agit d'une somme algébrique : il faut orienter le contour d'Ampère, et donc donner une normale à la surface, d'où une convention de signe concernant les courants enlacés, comptés positivement ou négativement selon leur sens.

• si le circuit enlace un courant surfacique k, alors l'intensité enlacée aura la forme suivante :

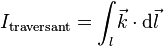
Bibliographie

• John David Jackson, Électrodynamique classique « trad. de (en)Classical Electrodynamics »