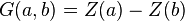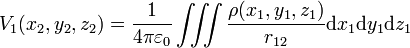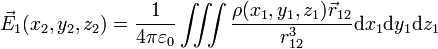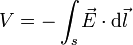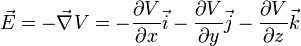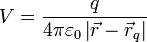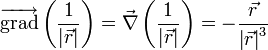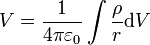Potentiel électrique - Définition

Introduction

Le potentiel électrique est l'une des grandeurs définissant l'état électrique d'un point de l'espace. Son unité est le volt. Le potentiel électrique est principalement utilisé afin de calculer les variations d'énergie potentielle de particules en mouvement ; ou encore pour trouver plusieurs valeurs inconnues dans les circuits électriques.

Analogie

On observe un courant d'eau dans une rivière:
C'est la différence d'altitude entre deux points du lit de la rivière :

qui fait qu'un courant existe entre ces deux points. L'altitude Z est un potentiel gravitationnel (on connaît l'énergie potentielle liée à l'altitude).

D'où l'analogie entre la dénivellation géographique et la différence de potentiel électrique appelée également tension et notée U.

La différence de potentiel (ou tension en l'absence de phénomènes d'induction d'origine extérieure) est une valeur algébrique (c'est-à-dire qu'elle peut être positive, négative ou nulle). On la représente sur les schémas électriques par une flèche allant d'un point B vers un point A lorsqu'on veut représenter le potentiel du point A par rapport à celui du point B.

.

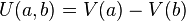
Formules

Le potentiel électrique en un point de l'espace est un concept du domaine de l'électricité. Il est défini à partir de la distribution des charges électriques dans l'espace à l'aide de l'application de la loi de Coulomb à une distribution volumique de charge et en utilisant le principe de superposition :

où : et où est la densité de charge en 1 (autour du point 1 il y a une charge dans le volume )

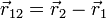
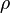
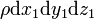
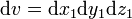
Le champ électrique qui dérive de ce potentiel est alors donné par la formule suivante :

Inversement, la connaissance du champ électrique en un point permet le calcul du potentiel dont il découle :

où est le potentiel électrique, et dl est l'élément d'intégration.

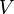
Cas particulier

Le potentiel électrique créé par une charge ponctuelle dans l'espace qui l'environne est :

où q est la charge ponctuelle, r est le vecteur de position du point où l'on calcule le champ et r_q est le vecteur position de la charge pontuelle.

Comme mathématiquement :

où est la densité de charge en fonction de la position et r est la distance de l'élément de volume dV.

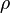
V est un scalaire .

Mesure

Sa mesure s'effectue en physique comme en biologie grâce à un voltmètre ou à un oscilloscope qui sont toujours placés en dérivation ou en parallèle, par rapport au circuit ou à l'objet bipolaire à mesurer.

Le potentiel est toujours défini à une constante près. En électricité il est fréquent que l'on prenne comme référence pour les potentiels (c'est-à-dire le potentiel qui sert de zéro) le potentiel de la terre (que l'on abrège par terre), même si cela n'est pas une obligation. Quel que soit le choix opéré, le point de référence dans le circuit dont le potentiel est fixé à 0 volt est appelé point froid. Selon les dispositifs il peut être relié soit à la masse (carcasse métallique du dispositif), soit à la terre, soit au deux.

Pour des explications plus pratiques concernant la notion de potentiel électrique, on se référera à l'article tension.

L'énergie potentielle

La variation d'énergie potentielle électrique d'une particule chargée se calcule à partir de la différence entre les potentiels à chacun des points. Il est possible de faire une analogie entre la hauteur et le potentiel. Lorsque la particule diminue en potentiel, son énergie potentielle diminue proportionnellement. Toutefois, contrairement à l'énergie potentielle gravitationnelle, l'énergie potentielle électrique dépend de la charge de la particule; et non de sa masse. Donc,

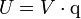
• U : Énergie potentielle électrique
• V : potentiel électrique
• q : charge élémentaire (négatif dans le cas d'un électron)