Théorème de Bachet-Bézout - Définition
La liste des auteurs de cet article est disponible ici.
Extension aux anneaux principaux quelconques
L'identité de Bézout peut s'écrire non seulement dans l'anneau des nombres entiers relatifs, mais aussi dans tout autre anneau principal. Notons que dans ce cas « plus grand diviseur » s'entend seulement au sens de la relation d'ordre fournie par la divisibilité dans l'anneau , l'unicité du pgcd n'est conservée qu'à un facteur inversible près de l'anneau. C'est-à-dire, si A est un anneau principal, et a et b sont des éléments de A non tous nuls, et d est un plus grand diviseur commun de a et b , alors il existe des éléments x et y dans A tels que :
Dans un anneau principal, un PGCD de a et b est un générateur de aA + bA, l'identité de Bézout est une conséquence de cette définition.
Identité de Bézout dans l'ensemble des polynômes
L'identité de Bézout se généralise à l'ensemble des polynômes à une indéterminée sur un corps commutatif K
Théorème — Étant donné une famille finie
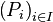
![\mathbb{K}[X]](https://static.techno-science.net/illustration/Definitions/autres/a/a54a58150f8fbfa21e4e47bea7551681_74473e1ff482d8b2fb4406e56cad5749.png)
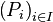
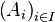
![\mathbb{K}[X]](https://static.techno-science.net/illustration/Definitions/autres/a/a54a58150f8fbfa21e4e47bea7551681_74473e1ff482d8b2fb4406e56cad5749.png)
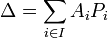
En particulier, les polynômes
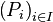
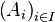
![\mathbb{K}[X]](https://static.techno-science.net/illustration/Definitions/autres/a/a54a58150f8fbfa21e4e47bea7551681_74473e1ff482d8b2fb4406e56cad5749.png)
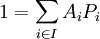
Extension à d'autres anneaux
L'identité de Bachet-Bézout a donné lieu à une classe d'anneaux : un anneau A est dit de Bézout si tout idéal de type fini de A est principal . Bien entendu l'identité de Bézout est valable dans tout anneau de Bézout.

















































