Anneau principal - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les anneaux principaux forment un type d'anneaux important dans la théorie mathématique de la divisibilité. Ce sont les anneaux intègres, commutatifs et unitaires non nuls auxquels on peut étendre deux théorèmes qui, au sens strict, concernent l'anneau des entiers relatifs : le théorème de Bachet-Bézout et le théorème fondamental de l'arithmétique.
Définitions
Un anneau A est dit unitaire s'il admet un élément neutre pour la multiplication. Il est dit intègre si pour tous éléments a et b de A tels que a.b soit égal à zéro, un au moins des éléments a et b est nul. Cette propriété a pour conséquence que tout élément non nul de A est simplifiable, c'est-à-dire que si a est un élément non nul de A, si b et c sont deux éléments de A tels que a.b = a.c (resp. b.a = c.a), alors b est égal à c. La simplification utilisée pour les calculs sur les nombres entiers, rationnels, réels ou complexe est donc toujours valable. Enfin l'anneau A est dit commutatif si, pour tous éléments a et b de A, a.b = b.a. Dans toute la suite de l'article, A désigne un anneau commutatif unitaire intègre.
Un idéal J est un sous-groupe de A stable par multiplication de n'importe quel élément a de A, ainsi si j est élément de J, a.j l'est aussi, ou encore a.J est inclus dans J. L'idéal J est dit principal s'il est composé des multiples d'un élément de l'anneau.
- Un idéal J de l'anneau A est dit principal si et seulement s'il existe un élément a de A tel que J est égal à a.A.
- Un anneau commutatif unitaire et intègre est dit principal si et seulement si tous ses idéaux sont principaux.
Propriétés
Arithmétique
L'arithmétique élémentaire sur l'anneau des entiers relatifs se fonde sur quelques théorèmes clés. A l'exception de la division euclidienne qui n'est pas définie dans le cas général d'un anneau principal, ces grands théorèmes s'appliquent encore dans ce contexte. Ils permettent de généraliser les raisonnements arithmétiques à tous les anneaux principaux.
Le théorème de Bachet-Bézout est encore vérifié :
- Si a et b sont deux éléments de A n'ayant pas d'autres diviseurs communs que les éléments du groupe des unités de l'anneau, alors il existe u et v éléments de A tels que a.u + b.v = 1.
Cette propriété résulte du fait que l'idéal engendré par a et b est principal, et tout générateur de cet idéal est diviseur commun à a et b, donc est inversible et engendre l'anneau tout entier. En particulier, l'élément 1 appartient à cet idéal, ce qui entraîne la relation.
Une fois établies les définitions de pgcd et ppcm, l'identité de Bézout prend une forme un peu différente : l'équation diophantienne ax+by = c admet des solutions si et seulement si c est un multiple du pgcd de a et de b.
Le lemme d'Euclide aussi est vérifié :
- Soit a, b et c trois éléments de A tel que a divise b.c et tel qu'il n'existe pas d'autres diviseurs commun à a et à b que les éléments du groupe des unités. Alors a est un diviseur de c.
En effet, l'identité de Bézout assure l'existence de deux éléments de A, u et v tel que a.u + b.v = 1. La multiplication par c des deux membres de cette égalité permet d'écrire (i) a.u.c + b.c.v = c. De plus, a est un diviseur de b.c, ce qui se traduit par l'existence d'un élément d de A tel que: (ii) b.c = a.d. Les égalités (i) et (ii) démontre l'égalité suivante: a.( u.c + v.d) = c. Ceci montre que a divise c et le lemme d'Euclide est bien vérifié.
Enfin, le théorème fondamental de l'arithmétique est vérifié :
- Un anneau principal est factoriel, c'est-à-dire que tout élément de l'anneau se décompose de manière unique (aux facteurs inversibles près) en un produit de facteurs irréductibles.
Une unité désigne un élément qui possède un inverse dans l'anneau. Un facteur irréductible de l'anneau est un élément p tel que chacune de ses décompositions en produit de deux facteurs contienne au moins une unité. Ainsi dans Z, -2 est irréductible car toute décomposition en un produit de deux facteurs contient nécessairement 1 ou -1 comme facteur. La décomposition est unique à un facteur inversible près. On remarque en effet qu'il existe plusieurs décompositions, par exemple de 6, 6 = 2 x 3 = (-2) x (-3). En revanche, ces deux décompositions sont les mêmes, à un facteur inversible près. Une démonstration est présentée dans l'article Anneau factoriel.
Idéal
- Un élément a est premier si et seulement si A/a.A est un corps.
Soit b un élément dont la classe dans l’anneau quotient est non nulle, alors b n'est pas élément de a.A. Comme a est premier, il n'existe pas d'autres diviseurs communs que les éléments du groupe des unités. L'identité de Bézout, par passage aux classes montre que b est inversible. L'idéal a.A est dit maximal, c'est-à-dire que les seuls idéaux contenant a.A sont lui-même et A tout entier.
Réciproquement si A/a.A est un corps, soit b un diviseur de a qui ne soit pas un élément inversible, alors il existe un élément c de l'anneau tel que b.c = a et la classe de b est un diviseur de zéro. Le seul diviseur de zéro d'un corps est zéro. Ceci montre que b est dans l'idéal a.A et b est un multiple de a. L'élément b est à la fois un diviseur et un multiple de a, ceci montre que c est inversible. Ainsi, tout diviseur de a non inversible est égal à a, à un facteur inversible près, ce qui démontre que a est premier.
On remarque que si a est premier l'idéal est aussi premier, on en déduit la proposition :
- Les idéaux premiers de A sont les idéaux maximaux.
Propriétés noethériennes
Un anneau principal est noethérien, c'est-à-dire qu'il vérifie la propriété suivante :
- Toute suite croissante d'idéaux est stationnaire.
En effet, si (Jn) est une suite croissante d'idéaux, l'union J de tous ces idéaux est un idéal (du fait que la suite est croissante). Soit a un générateur de J, il existe un entier N tel que JN contient a. On en déduit les inclusions suivantes :
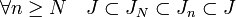
Ces inclusions montrent qu'à partir du rang N, la suite est constante égale à J. Elle est donc stationnaire.
La noethérianité entraîne de nombreuses propriétés ; les deux suivantes sont vraies pour tous les anneaux commutatifs, mais imposent l'usage d'une forme plus élaborée de l'axiome du choix pour une démonstration du cas général :
- Tout idéal distinct de l'anneau est inclus dans un idéal maximal.
En effet, si un idéal distinct de l'anneau n'est inclus dans aucun idéal maximal, il est possible de construire une suite croissante d'idéaux qui n'est pas stationnaire et l'anneau n'est pas noethérien (donc pas principal).
- Un élément de A est inversible si et seulement s'il n'appartient à aucun idéal maximal.
En effet, un élément a de A est non inversible si et seulement si l'idéal a.A est distinct de A c'est-à-dire, d'après la proposition précédente, si et seulement s'il est inclus dans un idéal maximal.
Anneau de Dedekind
Il existe un type particulier d'anneaux noethériens important en théorie des nombres, les anneaux de Dedekind.
Un anneau de Dedekind est un anneau A commutatif unitaire intègre et noethérien, dont tout idéal premier est maximal, et tel que A est intégralement clos, c'est-à-dire que les seuls éléments du corps des fractions de A qui sont entiers sur A sont les éléments A. (Rappelons qu'un élément est entier sur A si et seulement s'il est racine d'un polynôme unitaire à coefficients dans A.)
- Un anneau principal est intégralement clos.
On en déduit la proposition suivante :
- Un anneau principal est de Dedekind.
Soient A un anneau principal, K son corps des fractions et α / β un élément de K entier sur A, avec α et β deux éléments de A premiers entre eux. Dire que α / β est entier sur A revient à dire qu'il existe un entier n > 0 et des éléments a0, ... , an-1 de A, tels que :
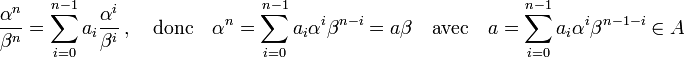
L'élément β est premier avec α, il est donc premier avec αn. Comme β divise αn on en déduit que β est un élément inversible de A, ce qui montre que α / β est élément de A et par voie de conséquence tout élément de K entier sur A est un élément de A.
L'anneau A est intégralement clos, les démonstrations précédentes montrent que tout idéal premier est maximal et l'anneau est noethérien, il est donc de Dedekind.
Module sur un anneau principal
Un module sur un anneau est aux anneaux ce qu'un espace vectoriel est à un corps. Un module sur un anneau A commutatif unitaire et intègre est un groupe abélien disposant d'une multiplication externe dotée des mêmes propriétés que celle d'un espace vectoriel.
- Un module est dit libre s'il admet une base. Il est dit de type fini s'il admet une famille génératrice de cardinal fini.
La situation n'est pas la même que celle d'un espace vectoriel. Un module de type fini n'admet pas nécessairement une base. Par exemple un groupe abélien fini G peut être aussi vu comme un Z module si z est un entier relatif et m un élément du module, z.m est égal à l'itérée m + m + ... + m z fois si z est positif et l'inverse de l'itéré -z fois si z est négatif. Toute famille finie (gi) de G admet une relation linéaire non triviale, si e est l'exposant du groupe G, e.g1 + e.g2 + ... est égal à zéro. Cette configuration est étudiée dans l'article groupe abélien de type fini.
Dans le cas d'un anneau principal A, la configuration est proche de celle des espaces vectoriels :
- Soit M un A module libre de type fini et de rang m, tout sous A module N de M admet une base de cardinal inférieur ou égal à m.
Une corollaire immédiat est le suivant :
- Un module libre de type fini sur un anneau principal est noethérien.
Dans le cas d'un anneau euclidien, il existe un algorithme effectif permettant de déterminer une base. Il se trouve dans l'article Théorème des facteurs invariants.
Raisonnons par récurrence sur m.
Si m est égal à zéro, le résultat est immédiat.
Supposons la propriété démontrée pour m - 1 et démontrons là pour m. Soient (ei) pour i variant de un à m une base de M et P le module libre engendré par la base (ei) pour i variant de un à m - 1. L'intersection de N et de P est, par hypothèse de récurrence un module libre de rang inférieur ou égal à m - 1. Soit (fi) pour i variant de un à n - 1 une base de l'intersection de N et de P.
Notons J l'ensemble des coordonnées de em utilisée dans l'écriture des éléments de N dans la base (ei). L'ensemble J est un idéal de A, il existe donc un élément g de A, tel que l'idéal J soit engendré par g, notons fn un élément g.em + p de N, où p est un élément de P. Par définition de J, un tel élément existe.
Si g est égal à zéro, alors N est inclus dans P et l'hypothèse de récurrence permet de conclure. Sinon, montrons que (fi) pour i variant de un à n est une base de N. La famille est libre, en effet soit la combinaison linéaire nulle suivante :
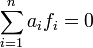
Soit pr la projection de M sur P parallèlement à A.em. L'image de la combinaison linéaire par pr est égale à an g.em. Comme g n'est pas nul, an l'est. La combinaison linéaire précédente se réduit à celle de la famille libre (fi) pour i variant de un à n - 1. Comme cette famille est libre et la combinaison linéaire est nulle, les coefficients sont tous nuls. On en déduit que la famille des coefficients est nulle, ce qui montre que la famille est libre.
Montrons que la famille est génératrice. Soit v un élément de N, si v est inclus dans P alors il est combinaison linéaire de la famille (fi), qui engendre l'intersection de N et de P. Sinon, il existe un élément a de A tel que la mième coordonnée de v dans la base (ei) soit égal à a.g. On en déduit que v - a.fn est un élément de l'intersection de P et de N et ce vecteur est combinaison linéaire de la famille (fi). On en déduit que v est engendré par la famille (fi) qui est donc génératrice.
La famille est libre et génératrice, c'est une base de N, ce qui termine la démonstration.

















































