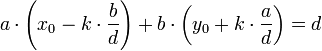Théorème de Bachet-Bézout - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Cet article parle de l'identité de Bézout et du théorème de Bézout en arithmétique. Pour le théorème de Bézout en géométrie algébrique voir Théorème de Bézout.
En mathématiques, le théorème de Bachet-Bézout ou identité de Bézout est un résultat d'arithmétique élémentaire, qui prouve l'existence de solutions à l'équation diophantienne linéaire :
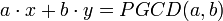
d'inconnues x et y entiers relatifs et où a, b sont des coefficients entiers relatifs et où PGCD(a,b) est le plus grand commun diviseur de a et b .
Le théorème de Bézout affirme que l'équation
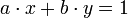
La première démonstration actuellement connue de ce théorème est due à Claude-Gaspard Bachet de Méziriac ; elle figure dans la seconde édition de son ouvrage Problèmes plaisans et délectables qui se font par les nombres, parue en 1624. Cependant, le mathématicien Étienne Bézout a généralisé ce résultat, notamment aux polynômes, démonstration notablement plus difficile. Par un de ces accidents de l'histoire mathématique, très fréquents, le nom de Bézout a été attribué à tort au résultat de Bachet.
Identité de Bézout dans l'ensemble des entiers relatifs
Théorème de Bachet de Méziriac

Théorème — Étant donnés deux entiers relatifs a et b pas tous nuls, si d est le PGCD de a et de b alors il existe deux entiers relatifs x et y tels que
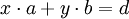
En particulier, deux entiers relatifs a et b sont premiers entre eux si et seulement s'il existe deux entiers relatifs x et y tels que
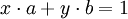
L'algorithme d'Euclide étendu, en fournissant un couple d'entiers solution de l'équation ax + by = pgcd(a,b), prouve déjà l'existence de solution à l'équation. Mais la démonstration qui suit, plus proche de celle qui sera utilisé dans les anneaux principaux, possède aussi un intérêt.
On peut supposer par exemple a non nul.
- Si
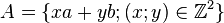
- En effet
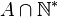
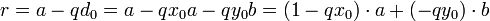
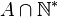
- Enfin, soit d un autre diviseur commun à a et b. Comme d divise a et b, d divise x0a + y0b donc d divise d0. d0 est bien le plus grand diviseur commun de a et b et il existe deux entiers x0 et y0 tels que pgcd(a,b) = ax0 + by0.
Remarque : si a et b sont nuls ils sont divisibles par n'importe quel entier et le pgcd n'existe pas.
Ce théorème ne possède en général pas de réciproque : l'existence de deux entiers tels que d = ax + by n'assure pas que d soit le PGCD de a et b. Il suffit pour s'en convaincre de remarquer, par exemple, qu'il existe deux entiers x et y tels que 2x + 3y = 5 alors que 5 n'est pas le PGCD de 2 et 3. S'il existe deux entiers x et y tels que d = ax + by, on peut seulement dire que d est un multiple du PGCD. En effet, a et b étant des multiples de leur PGCD, ax + by est un multiple du PGCD donc si d = ax + by alors d est un multiple du PGCD de a et b.
Dans le cas de l'équation ax+by = 1, il existe cependant une réciproque : l'existence de deux entiers x et y tels que ax + by = 1 assure que 1 est un multiple du PGCD de a et b. Cela ne se peut que si le PGCD de a et b est 1 donc seulement si a et b sont premiers entre eux.
Le théorème de Bachet-Bézout assure l'existence d'un couple d'entier tels que ax + by = PGCD(a,b). L'algorithme d'Euclide étendu fournit un des couples solutions, mais il en existe, en général, une infinité d'autres..
Par exemple, le plus grand diviseur commun de 12 et 42 est 6, et on peut écrire
mais aussi
-
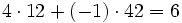
Si le PGCD d est non nul, à partir d'un couple solution (x0,y0), il est facile de prouver que l'on a aussi :
où k peut varier dans
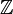
Applications
Le théorème de Bachet -Bézout intervient dans de nombreux domaine de la théorie des nombres.
- Il permet de démontrer le théorème de Gauss.
- Il intervient dans la recherche d'inverse modulo b et est donc utile dans le décodage de message en cryptographie.
- Il intervient dans la résolution de l'équation diophantienne ax+by = c.
Généralisation
Théorème — Étant donnés des entiers relatifs a1, ..., an non tous nuls, si d est le PGCD de a1, ..., an alors il existe des entiers relatifs x1, ..., xn tels que
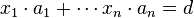
En particulier, a1, ..., an sont premiers entre eux (dans leur ensemble) si et seulement s'il existe des entiers relatifs x1, ..., xn tels que

En d'autres termes, quand les ai ne sont pas tous nuls, le PGCD de a1, ..., an est le plus petit entier strictement positif qui peut s'écrire comme combinaison linéaire, à coefficients entiers, de a1, ..., an.