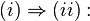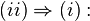Théorème de Pascal - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Il existe plusieurs théorèmes appelés théorème de Pascal.
Géométrie
Le théorème de Pascal est un théorème de géométrie projective.
Nous travaillons donc dans un plan projectif sur un corps (commutatif) quelconque K.
Théorème de Pascal (direct et réciproque)
- Il y a équivalence entre les 2 propositions suivantes concernant un hexagone d'un plan projectif
- (i) L'hexagone est inscrit dans une conique
- (ii) Les intersections des paires de côtés opposés sont alignées (voir (*) ci-dessous).
(*) Si 2 côtés opposés sont confondus, leur intersection n'est évidemment pas unique. Le théorème s'interprète alors par exemple en écrivant la seconde condition sous la forme: "Il existe une droite contenant 3 points appartenant aux intersections respectives des paires de côtés opposés". Cependant cette disposition ne peut exister dans le cas d'une conique propre puisque l'intersection d'une telle conique et d'une droite comporte au plus 2 points.
M1,M2,M3,M4,M5,M6 désignant les 6 sommets de l'hexagone, les paires de côtés opposés sont
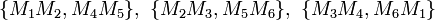
Il résulte des propriétés des homographies sur une conique que le birapport du faisceau de droites
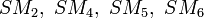
![[M_1M_2, \ M_1M_4, \ M_1M_5, \ M_1M_6]=[M_3M_2, \ M_3M_4, \ M_3M_5, \ M_3M_6]](https://static.techno-science.net/illustration/Definitions/autres/1/1eab1f7b985548b60c8fac39ca8e975a_12425a92e356986c4a9044b4d7ea765c.png)
En considérant respectivement les intersections de ces 2 faisceaux par les droites
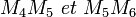
![[A, M_4, M_5, P] \ = \ [B, Q, M_5, M_6]](https://static.techno-science.net/illustration/Definitions/autres/a/a6af43cf5c3cfd96b39108c74bc27ad0_b4c99c76ab8b0fe8c16c9f695653a3f4.png)
Les droites
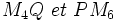
![[A, M_4, M_5, P] \ = \ [B', Q, M_5, M_6]](https://static.techno-science.net/illustration/Definitions/autres/4/463cb8244d51d5d9cd52c7f970718587_4670a99d4ef003b4ca6d02aef71e2c17.png)
![[B, Q, M_5, M_6] \ = \ [B', Q, M_5, M_6]](https://static.techno-science.net/illustration/Definitions/autres/6/6aed289ca369b8ba89731d3f9678a839_e95f00c7587d31afda1fa6aaebee4b7a.png)
Par hypothèse on a une projection de sommet C de la droite M4M5 sur M5M6 qui transforme M4 en Q, P en M6 , laisse M5 invariant et transforme A en B. Il en résulte l'égalité des birapports :
![[A, M_4, M_5, P] \ = \ [B, Q, M_5, M_6]](https://static.techno-science.net/illustration/Definitions/autres/a/a6af43cf5c3cfd96b39108c74bc27ad0_b4c99c76ab8b0fe8c16c9f695653a3f4.png)
![[M_1M_2, \ M_1M_4, \ M_1M_5, \ M_1M_6]=[M_3M_2, \ M_3M_4, \ M_3M_5, \ M_3M_6]](https://static.techno-science.net/illustration/Definitions/autres/1/1eab1f7b985548b60c8fac39ca8e975a_12425a92e356986c4a9044b4d7ea765c.png)
Là encore les propriétés des homographies sur une conique montrent que les 6 points M1,M2,M3,M4,M5,M6 appartiennent à une même conique.
Théorème de Pappus-Pascal
Ce théorème est un cas particulier du théorème (direct) de Pascal. Il s'agit de celui où la conique est dégénérée en 2 droites distinctes D et D'. De plus, pour obtenir un résultat non trivial (vérification immédiate), on suppose que les 2 sommets de chaque côté appartiennent à des droites D, D' distinctes.
On peut remarquer en reprenant la démonstration dans ce cas que les résultats généraux d'homographie sur une conique ne sont pas réellement utilisés. Les théorèmes invoqués sont plus simplement ceux concernant les divisions de points alignés et les faisceaux de droites.
Théorème de Pascal (2)
- Théorème de PASCAL
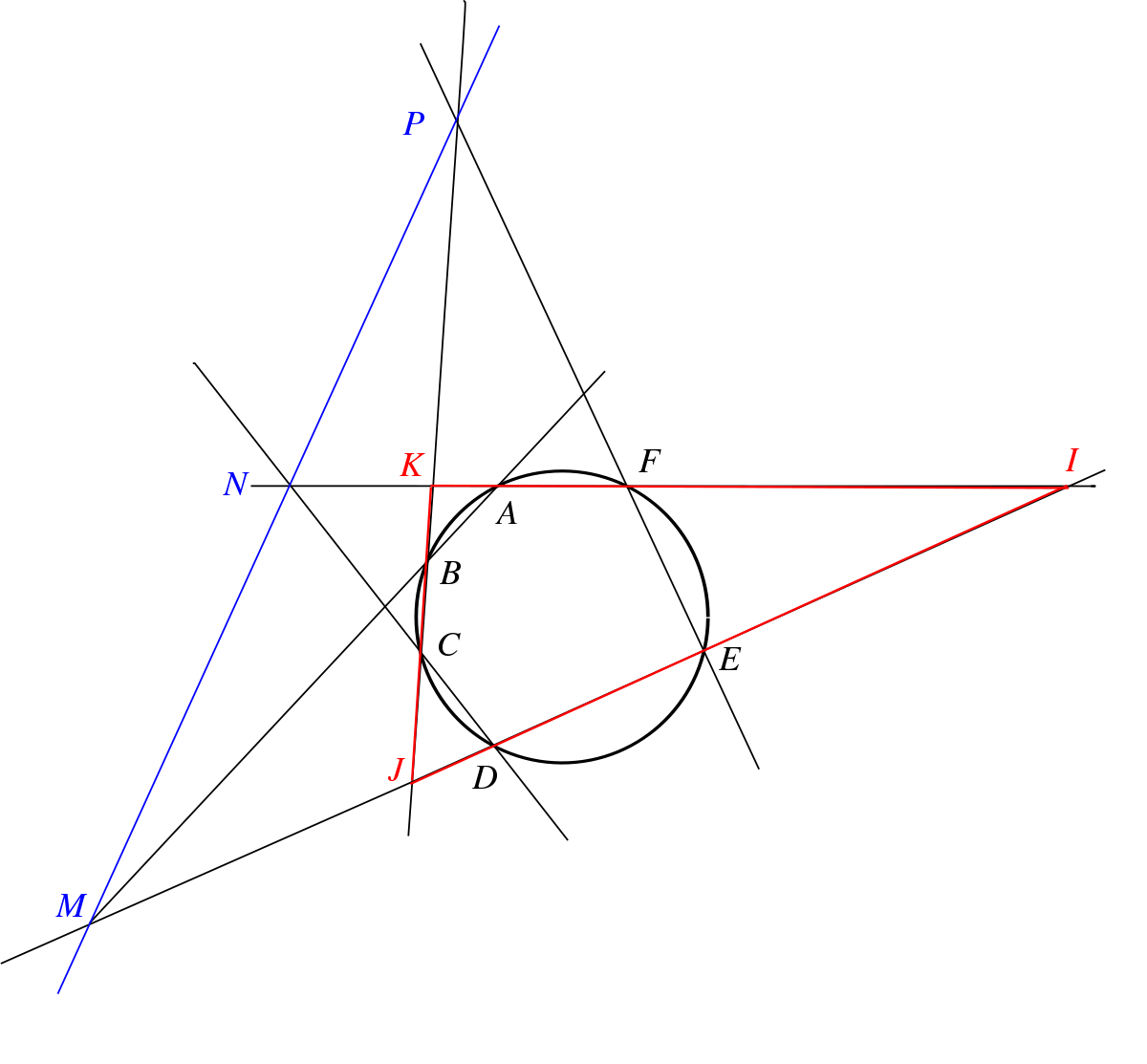
- Étant donné un hexagone inscrit dans un cercle, les intersections des côtés opposés sont alignées.
On veut prouver l'alignement de M,N,P; on utilisera donc le théorème de Ménélaüs. Un triangle envisageable pour ce théorème est obtenu avec les droites (BC),(DE),(FA) qui donnent les points I,J,K (un autre celui construit avec (AB),(CD),(EF)). Les côtés non utilisés de l'hexagone fournissent des points alignés avec M,N,P, d'où des utilisations possibles de Menelaüs qui traduisent en fait la façon dont la figure est construite. Il suffit alors d'utiliser le fait que tous ces points sont sur un même cercle, ce qui justifie l'utilisation de la puissance d'un point.
On veut donc calculer
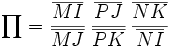
En utilisant le théorème de Ménélaüs dans le triangle IJK et le fait que M,A,B soient alignés on tire
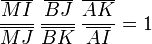
d'où
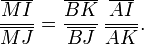
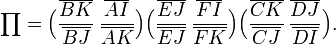
En utilisant la puissance de I,J,K par rapport au cercle, on tire
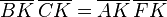
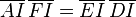
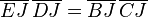
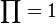
La droite que forme cet alignement est appelée droite de Pascal. La figure obtenue par la construction est appelée hexagramme mystique.
En prenant la polaire de cet énoncé par rapport au cercle lui-même, nous obtenons l'énoncé dit "dual" du précédent
| Énoncé initial | Énoncé "polarisé" |
|---|---|
| six points | six tangentes |
| point d'intersection | droite joignant |
| côté opposé | sommet opposé |
| aligné | concourante |
- Théorème de Brianchon
- Étant donné un hexagone circonscrit à un cercle, les diagonales sont concourantes.
Ci-dessous le dessin dual du précédent. Les points ont été remplacés par les tangentes correspondantes ; le point de concours est le pôle de la droite précédente, ce qui est mis en évidence avec la tangente au cercle issue du projeté sur la droite du centre du cercle (en pointillé).
Prenant maintenant la polaire de ces deux énoncés par rapport à un cercle quelconque nous obtenons que ces deux énoncés restent valables sur une conique quelconque au lieu d'un cercle.
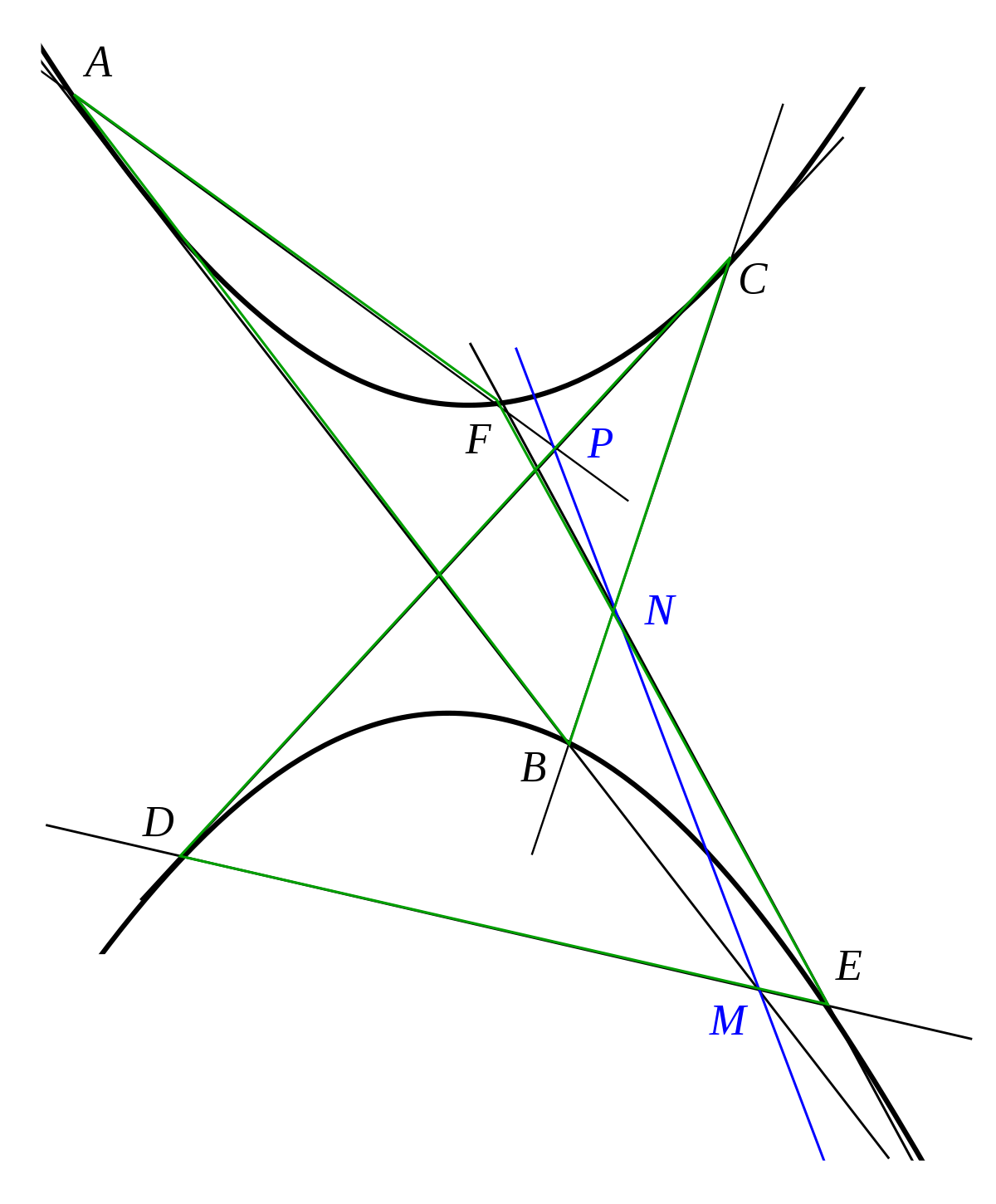
Ci-dessous le théorème de Pascal pour une hyperbole dans une situation "croisée" : non seulement l'hexagone n'est pas convexe, mais les côtés se croisent.
La réciproque de ce théorème est vraie également : si les trois points A, B, C d'intersection des côtés opposés de l'hexagone sont alignés alors l'hexagone est inscrit dans une conique.
Développements
Pour de plus amples informations et de très nombreuses constructions géométriques, nous renvoyons le lecteur au site cabri.imag déjà mentionné.
On trouvera également sur cette page une autre démonstration n'utilisant pas la transformée par polaires réciproques, mais l'écriture barycentrique d'une conique. Le résultat s'obtient alors par annulation d'un déterminant.
Réciproque du théorème de Pascal
Le théorème de Branchion admet une réciproque qui permet de définir les coniques d'une façon purement formelle en géométrie projective formelle (cf. traité projectif des coniques). On en trouvera ici une démonstration utilisant l'écriture barycentrique des coniques.
Nous en proposons une totalement analytique.
On se donne six points A,B,C,A',B',C'.
On prend comme repère A,B,C. Une conique passant par A,B,C admet une équation de la forme
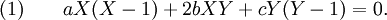
On note α,α' les coordonnées de A' (etc).
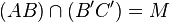
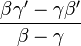
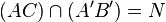
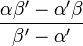
Au lieu de calculer les coordonnées de
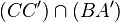
Équation de (CC') :
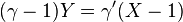
Équation de (BA') :
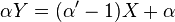
Équation de (MN) :
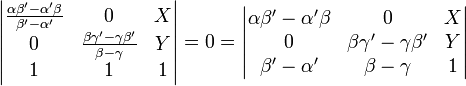
La concourance se traduit par la nullité du déterminant
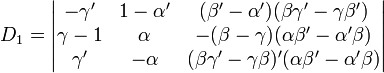
Maintenant, le fait que les points A',B',C' soient sur la conique d'équation (1) se traduit par un système de trois équations (une par point) d'inconnues a,b,c et qui admet une solution non triviale. Ceci se traduit par la nullité du déterminant
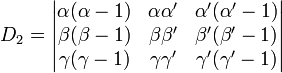
Miracle ! Ces deux déterminants sont égaux !
On peut bien sûr les calculer par la méthode de Sarrus, mais on peut aussi observer que dans D2, le terme αα' (etc) n'apparaît que dans la deuxième colonne son facteur valant
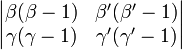
Nous calculons ce facteur dans D1 en utilisant la deuxième colonne :
---
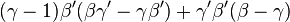
---
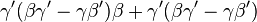
---
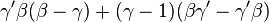
La somme donne la même expression que dans D2.
En échangeant α' et γ, β,β' et α,γ' les déterminants ne changent pas ce qui permet d'affirmer l'égalité des coefficients de γγ'.
Reste celui de ββ', qui vaut
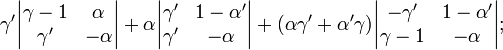
soit finalement le même que dans D1 une fois effectué le petit calcul.