Théorème de Wilson - Définition

Histoire

Le premier texte à faire référence à ce résultat est énoncé par le mathématicien arabe Alhazen , démontrant une remarquable avance sur les sciences occidentales. Ce théorème est connu à partir du XVII^e siècle en Europe. Gottfried Wilhelm von Leibniz fait référence à ce résultat sans le démontrer. John Wilson redécouvre ce qu'il croit être une conjecture et en partage la découverte avec son professeur Edward Waring qui publie cette conjecture en 1770.

Trois ans plus tard, Joseph-Louis Lagrange en publie une première démonstration et Leonhard Euler en présente une deuxième. Utilisant les notations de l'arithmétique modulaire, Carl Friedrich Gauss reformule les démonstrations de Lagrange et d'Euler et en donne une troisième.

Généralisation

Dans un groupe abélien fini le produit des éléments est égal

• au neutre si l'ordre du groupe est impair
• au produit des éléments d'ordre 2 si l'ordre du groupe est pair.

Pour le groupe , avec p premier impair, on retrouve le version classique.

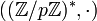
En effet, son ordre, qui est égal à p-1, est pair et son unique élément d'ordre 2 est la classe (modulo p) de -1.