Théorème de la progression arithmétique - Définition
La liste des auteurs de cet article est disponible ici.
Démonstration
Ici, n désigne un nombre strictement positif et m une classe du groupe des unités de l'anneau Z/nZ. L'objectif est de montrer que m contient une infinité de nombres premiers. P désigne l'ensemble des nombres premiers, S le demi-plan complexe dont tous les éléments ont une partie réelle est strictement supérieure à 1 et s un nombre complexe élément de S. Si c désigne un complexe, c* désigne son conjugué.
Le groupe des unités de Z/nZ est désigné par la lettre U, un caractère de Dirichlet par le symbole χ et le groupe des caractères
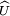
La fonction ω (s,u)
L'objectif est de définir une fonction ω, définie dans SxU dont le comportement détermine le cardinal de l'ensemble des nombres premiers inclus dans m.
-
- La fonction ω, de SxU dans l'ensemble des nombres complexes et définie par la formule suivante est absolument convergente sur son domaine de définition.
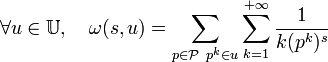
-
- Si m ne contient qu'un nombre fini de nombres premiers alors ω possède une limite en (1, m).
Une fois cette proposition établie, il suffit de montrer que la fonction diverge en un pour démontrer le théorème.
-
- La fonction ω est absolument convergente sur son domaine de définition.
Cette proposition est démontrée dans le paragraphe Produit eulérien de l'article détaillé.
-
- Si m ne contient qu'un nombre fini de nombres premiers alors ω possède une limite en (1, m).
Il suffit pour s'en rendre compte, de diviser la somme en deux et de montrer que le deuxième terme est absolument convergent autour de la valeur un.
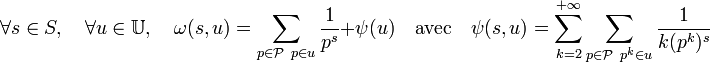
On remarque que ψ(s, u) est majoré par un, en effet :
Délocalisation des nombres premiers
La difficulté réside dans le fait que la sommation n'est réalisée que sur les nombres premiers inclus dans m. Euler fournit bien une mesure des nombres premiers, mais elle couvre intégralement Z.
Cependant, la fonction ω dépend d'un paramètre u élément d'un groupe abélien fini. Or un tel groupe possède une analyse harmonique puissante, les fonctions trigonométriques sont remplacées par les caractères et l'on dispose d'une transformée de Fourier et du théorème de Plancherel, il permet de délocaliser l'ensemble des nombres premiers :
-
- La fonction ω est égale à l'expression suivante sur son domaine de définition :
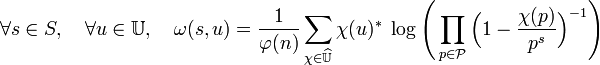
La démonstration est donnée dans le paragraphe Produit eulérien de l'article Caractère de Dirichlet.
Produit eulérien
L'expression contient un produit eulérien, il est cependant plus simple de traiter une série traditionnelle. Or Euler a établi un calcul permettant une transformation des produits de ce type en série plus classique.
-
- La fonction ω est égale à l'expression suivante sur son domaine de définition :
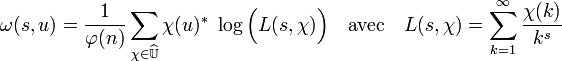
La démonstration est donnée dans le paragraphe Caractère de Dirichlet de l'article détaillé.
Série L de Dirichlet
La constante χ(u)* est une racine de l'unité, elle ne s'annule donc jamais. Il reste à connaitre le comportements des fonctions L(s, χ) autour du point un. Ces fonctions sont appelées série L de Dirichlet. Si χ est le caractère principal, il est proportionnel à la fonction zêta de Riemann et est en conséquence divergeant au point un. En revanche, si χ n'est pas le caractère principal sa série associée est définie et non nulle en un. Ce qui permet d'énoncer la proposition suivante :
-
- Pour toute valeur de u dans le groupe des unités différente de un, la fonction ω converge quand s tend vers un vers une valeur différente de zéro.
La démonstration est donnée dans le paragraphe Comportement au point un de l'article détaillé.
Ceci permet de conclure. Si m ne contenait qu'un nombre fini de nombres premiers alors la fonction ω convergerait d'après le premier paragraphe de la démonstration. Or elle diverge car elle est somme d'une fonction divergente et d'un nombre fini de fonctions convergentes.

















































