Caractère de Dirichlet - Définition

Introduction

Johann Peter Gustav Lejeune Dirichlet

En mathématiques, et plus précisément en arithmétique modulaire, un caractère de Dirichlet est une fonction souvent notée χ de l'ensemble des congruences sur les entiers dans l'ensemble des nombres complexes particulière.

Elle a été découverte par Dirichlet pour la démonstration de son théorème de la progression arithmétique.

Définitions

Dans cet article n désigne un entier strictement positif. Il existe deux définitions d'un caractère de Dirichlet :

• Un caractère de Dirichlet, souvent noté χ, est un morphisme du groupe des unités de l'anneau Z/nZ à valeurs dans le groupe des nombres complexes de module 1.

Selon cette définition un caractère de Dirichlet est simplement un caractère du groupe des unités de l'anneau Z/nZ au sens des caractères des groupes.

Il existe une deuxième définition, le caractère est alors une fonction arithmétique :

• Un caractère de Dirichlet χ est une fonction de l'ensemble N^* des entiers strictement positifs dans C, totalement multiplicative, périodique. Si n est la période et d un entier strictement positif, χ(d) est de module 1 si d est premier avec n et nul sinon.

Les deux définitions sont un peu équivalentes. Si χ est un caractère au sens de la première définition et d un entier, au sens de la deuxième définition χ(d) est nul si la classe de d dans Z/nZ n'est pas élément du groupe des unités et vaut l'image par χ de sa classe sinon.

• Le conducteur d'un caractère de Dirichlet est l'entier n définissant l'anneau Z/nZ.

• Un caractère de Dirichlet est dit primitif si et seulement si son noyau est réduit à l'élément neutre.

• Le caractère de Dirichlet valant 1 sur les entiers premiers avec n et 0 ailleurs est appelé caractère principal de conducteur n.

• Le caractère de Dirichlet valant 1 sur tous les entiers est dit caractère trivial.

Théorème de la progression arithmétique

Produit eulérien

L'objectif initial des caractères de Dirichlet est de dénombrer les nombres premiers dans une classe x de Z/nZ ce qui revient à démontrer le théorème de la progression arithmétique. On remarque que, à l'exception des diviseurs premiers de n, qui sont en nombre fini, ces nombres premiers se trouvent tous dans les classes du groupes des unités noté U. Il est donc utile de choisir x une classe inversible.

Dirichlet cherche une fonction ω de DxU où D désigne le demi-plan complexe des nombres dont la partie réelle est strictement supérieure à un et à valeurs complexes. La valeur en (s, x) doit fournir suffisamment d'informations pour conclure. Il choisit la fonction suivante, où P désigne l'ensemble des nombres premiers :

Le théorème de Plancherel permet une expression plus agréable de l'expression :

La formule finale possède un avantage : le produit n'est plus limité aux nombres premiers inclus dans la classe x mais à tous les nombres premiers. Un tel produit porte le nom de produit eulérien.

Ici, s désigne un nombre complexe dont la partie réelle est strictement supérieure à un et x une classe du groupe des unités U. Avant d'établir les convergences, définissons P _l comme l'ensemble des l premiers nombres premiers et m un entier strictement positif. Soit alors ω_lm la fonction définie par :

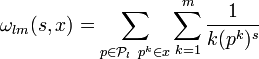
La transformée de Fourier de ω_lm, pour le caractère χ, est définie par :

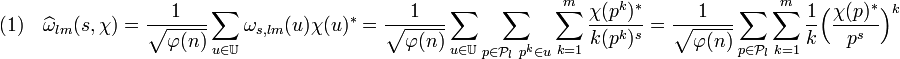
La série suivante est absolument convergente car la norme de la valeur d'un caractère est égale à un et p ^s est, en module, strictement supérieur à un. Elle converge vers un logarithme complexe noté ici log. Le logarithme choisi est tel que l'image de un est égal à zéro et il est bien défini sur le disque de centre un et de rayon un demi.

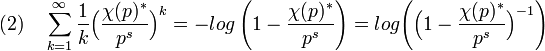
On en déduit que la suite qui à m associe est absolument convergente, soit sa limite. L'égalité (1) devient, avec l'expression de l'égalité (2) :

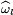
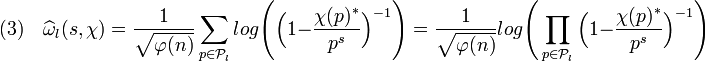
La majoration suivante montre que la suite ( ) est absolument convergente :

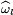
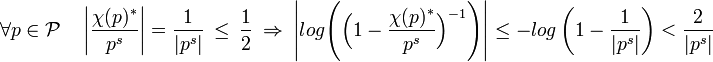
Soit la limite on obtient, à partir de la formule (3) :

Ce qui termine la démonstration.

 

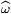
Séries L de Dirichlet

Les techniques associés au produit eulérien permettent d'exprimer le produit précédent sous une forme plus plaisante :

• La fonction L(s, χ) est appelée série L de Dirichlet du caractère χ.

La convergence est absolue si s est un nombre complexe avec une partie réelle > 1. Par prolongement analytique, cette fonction peut être étendue à une fonction méromorphe sur le plan complexe entier.

Les séries L de Dirichlet sont les généralisations directes de la fonction zêta de Riemann et apparaissent comme prééminentes dans l' hypothèse de Riemann généralisée.