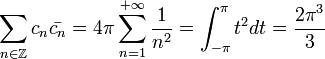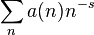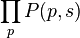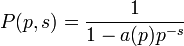Produit eulérien - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus précisément en théorie analytique des nombres, un produit eulérien est un développement en produit infini, indexé par les nombres premiers.
Il permet de mesurer la répartition des nombres premiers et est intimement lié à la fonction zêta de Riemann.
Il est nommé en l'honneur du mathématicien suisse Leonhard Euler .
Autres produits eulériens
Caractère de Dirichlet
Dirichlet souhaite démontrer que les nombres premiers dans une classe m de Z/nZ sont en nombre infini, si m et n sont premiers entre eux. Il utilise les caractères portant maintenant son nom et, au cours d'un calcul explicité dans le paragraphe Produit eulérien de l'article détaillé, aboutit sur le produit suivant :
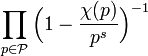
Ici χ désigne un caractère de Dirichlet, l'ensemble des caractères est noté
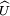
![\forall s \in ]1, +\infty[ \quad \forall \chi \in \widehat U \quad L(s, \chi) = \sum_{k=1}^{\infty} \frac {\chi(k)}{k^s} \ = \ \prod_{p \in \mathcal P} \Big(1 -\frac {\chi(p)}{p^s}\Big)^{-1}](https://static.techno-science.net/illustration/Definitions/autres/7/7f096f5e3a46fa757395901c4d1ffb5c_edba23cf4b162de4e291d88637ed8e79.png)
En effet, la fonction χ est complètement multiplicative, le calcul d'Euler s'applique de la même manière.
-
- La fonction L(s, χ) est appelée série L de Dirichlet du caractère χ.
La convergence est absolue si s est un nombre complexe avec une partie réelle > 1. Par prolongement analytique, cette fonction peut être étendue à une fonction méromorphe sur le plan complexe entier.
Les séries L de Dirichlet sont les généralisations directes de la fonction zêta de Riemann et apparaissent comme prééminente dans l' hypothèse de Riemann généralisée.
Généralisation
En général, une série de Dirichlet de la forme
où
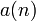
où
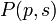
-
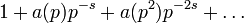
En fait, si nous considérons cela comme des fonctions génératrices formelles, l'existence d'un tel développement formel en produit eulérien est une condition suffisante et nécessaire pour que
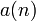
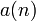
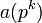
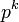
Dans la pratique, tous les cas importants sont tels que la série infinie et le développement en produit infini sont absolument convergents dans une certaine région
- Re(s) > C :
c’est-à-dire dans un certain demi-plan droit des nombres complexes. Cela nous donne déjà quelques informations, puisque le produit infini, pour converger, doit donner une valeur différente de zéro ; donc la fonction donné par la série infinie n'est pas zéro dans un tel demi-plan.
Un cas particulier important est celui dans lequel
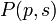
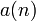
comme c'est le cas pour la fonction zêta de Riemann (avec
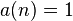
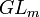
Travaux d'Euler
Calcul d'Euler
Euler cherche à évaluer la répartition des nombres premiers dont l'ensemble est ici noté P. Pour cela, il établit la formule suivante :

Ici Re(s) désigne la partie réelle de s.
Euler donne au terme de gauche le nom de fonction zeta, elle est définie sur le demi-plan complexe par :

Cette fonction se prolonge analytiquement sur l'ensemble du plan complexe en une fonction méromorphe.
Soit k un entier strictement positif, Pk l'ensemble des k premiers nombres premiers et Nk l'ensemble des entiers strictement positifs dont la décomposition en facteurs premiers ne comporte que des nombres premiers de l'ensemble Pk. Les éléments de Pk sont notés p1, ..., p k. L'exposant maximal de la décomposition en facteurs premiers d'un entier n est noté E(n).
La notation α désigne ici un k-uplet (α1, α2, ..., αk) d'entiers positif et N(α) désigne la valeur maximale atteinte par le k-uplet.
Enfin, s désigne un nombre complexe dont la partie réelle est strictement supérieure à 1 et l un entier strictement positif. L'objectif est de calculer la somme S kl(s), définie par :
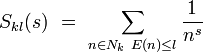
Un double passage à la limite, d'abord sur l puis sur k permet de conclure. On remarque en effet que la somme s'écrit aussi :
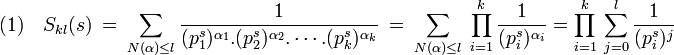
Chacune des k sommes du produit obtenu est absolument convergente. On en déduit :

La série en l de la majoration (2) est donc absolument convergente, on en déduit l'égalité :
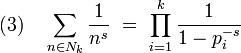
La série en k de l'égalité (3) est aussi absolument convergente, on en déduit :

Première distribution des nombres premiers
L'objectif est de déterminer une première loi sur la fréquence des nombres premiers. Il devient ainsi possible, par exemple, de répondre à la question : sont-ils plus ou moins nombreux que les carrés parfaits. Cette proposition doit se lire au sens où, si N est un entier suffisamment grand, existe-t-il plus de carrés parfaits inférieurs à N ou moins ? Euler répond à cette question en démontrant la divergence de la suite suivante :
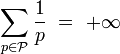
Ainsi, si pour tout n, il existait un nombre N plus grand que n tel que le nombre de nombres premiers soit supérieur au nombre de carrés parfaits, alors la série de terme général 1/n2 divergerait, ce qui n'est pas le cas.
L'objectif est alors de trouver un équivalent à la suite des nombres premiers. Il est donné par le théorème des nombres premiers.
L'égalité suivante montre que, si s tend vers 1, la fonction ζ diverge :
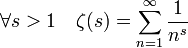
Ici ln désigne le logarithme naturel. La concavité de la fonction logarithme montre que :
![\forall x \in ]0,1-e^{-1}[ \quad x > -(1-e^{-1})\ln (1-x)](https://upload.wikimedia.org/math/b/9/8/b983a7de2006522eabe3d59f3e611648.png)
Si p est un nombre premier, il est supérieur à (1 - e-1)-1 et :

Le produit eulérien permet d'en déduire la majoration suivante :

La majoration (1) montre que si s tend vers 1, le terme de droite tend vers l'infini et donc aussi celui de gauche, ce qui démontre la proposition.
Calcul pour s égal à 2
Euler parvient à déterminer la valeur de la fonction ζ pour s égal à deux. Le calcul s'obtient très simplement avec l'aide des outils de l'analyse harmonique. Il suffit pour cela d'appliquer l'égalité de Parseval à la transformée de Fourier de la fonction périodique, notée f, de période 2π et égale à l'identité sur [-π, π[. On obtient :
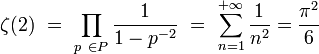
Euler établit ainsi une étrange relation entre un produit infini, construit avec des nombres premiers, et l'aire de la surface d'un cercle. Le problème de la sommation de la série associée était connue depuis longtemps sous le nom de Problème de Mengoli. Il fut résolu par Euler en 1735
Calculons les coefficients (cn) de la transformée de Fourier de f. Comme elle est impaire, le coefficient c0 est nul.
Le calcul de cn se traduit, en utilisant une intégration par partie, par :
![c_n = \frac 1{\sqrt {2\pi}}\int_{-\pi}^{\pi} t \ e^{(-int)} dt = \frac 1{\sqrt {2\pi}}\left[ \frac in t\ e^{(-int)}\right]_{-\pi}^{\pi} - \frac 1{\sqrt {2\pi}}\int_{-\pi}^{\pi} \frac in e^{(-int)} dt = (-1)^n\ \frac {i\sqrt {2\pi}}n](https://static.techno-science.net/illustration/Definitions/autres/1/17b373d66961e2e5ec377753d7faac92_459909bc0da1a1d10181e4612f4ac1aa.png)
L'égalité de Parseval permet d'établir que :