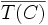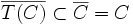Théorème du point fixe de Schauder - Définition

Introduction

Le théorème de Schauder, prouvé en 1930 par le mathématicien polonais Juliusz Schauder est un puissant théorème du point fixe intervenant dans la démonstration de l'existence de solutions à une équation différentielle.

Énoncé

Soit E un espace vectoriel normé sur , une partie non vide de E, convexe, fermée et bornée.

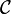
Si T est une application continue de C dans C telle que T(C) soit relativement compact, alors T a un point fixe

Preuve

Notons la norme de E.

Soit 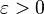. T(C) étant une partie relativement compacte de C, il est précompact, on peut donc recouvrir T(C) à l'aide d'un nombre fini de boules de rayon . Autrement dit, il existe un nombre entier, et dans C tels que :

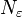
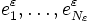
On définit alors pour tout l'application π_i,ε de C dans par :

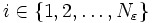
Chacune de ces applications est bien continue. On définit alors l'application continue par :

Tout d'abord, cette formule est bien définie, car le dénominateur n'est jamais nul. En effet, T(e) est dans l'une des boules et donc pour ce i, .

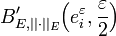
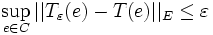
Par ailleurs . En effet, en notant , on vérifie que si , et :

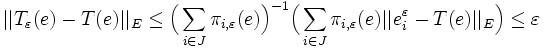
Posons alors . La définition même de nous assure que .

est un sous-ensemble fermé, borné, convexe, symétrie, inclus dans le sous-espace de dimension finie . On peut donc extraire de une base de G. Supposons à présent que contient plus de deux éléments. Alors . Montrons que 0 est à l'intérieur de , considéré en tant que partie de G. Les normes sur G étant équivalentes (G est de dimension finie), on peut considérer la norme N définie par . Si , on peut écrire , où . Posons alors x_i = δ_i | x_i | , où , alors , donc x est barycentre convexe des δ_ie_i qui sont dans (on rappelle que est symétrique et convexe). Il en résulte que contient la boule pour N de centre 0 et de rayon 1. 0 est bien à l'intérieur de

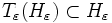
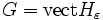
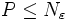
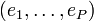
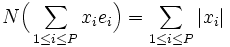
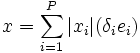
On définit l'application ρ de G dans par la formule :

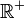
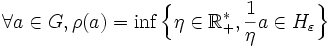
Tout d'abord, comme 0 appartient à l'intérieur de G, la fonction ρ est bien définie. On montre (par un raisonnement fastidieux, mais non difficile) que c'est une norme pour G, dont la boule unité n'est rien d'autre que . Ainsi est homéomorphe à la boule unité de (dans le cas où P = 0, c'est évident), et l'application directe du théorème du point fixe de Brouwer dit qu'il existe un vecteur tel que .

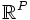
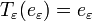
On peut appliquer tout ce long raisonnement pour , on dispose alors d'une suite d'éléments (x_n) de C tels que :

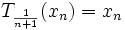
D'autre part, on sait que . Comme T(C) est relativement compact, est compact, on peut extraire de (T(x_n)) une sous-suite (T_σ(n)) convergente. Notons e sa limite, on a alors donc T(e) = e. e est bien dans C car .