Boule (mathématiques) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

En topologie, une boule est un sous-ensemble particulier d'un espace métrique. Le nom évoque, à juste titre, un objet familier dans $\R^3$ et plus généralement dans $\R^n$ muni de la distance euclidienne usuelle. Cependant, les boules peuvent avoir des " comportements " étranges dans les espaces métriques généraux, et ne pas être bien " rondes " dans les espaces vectoriels normés.

Définition générale

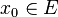
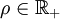
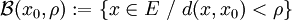
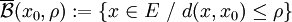
Dans un espace métrique $(E, d)$ , pour $x_0\in E$ et $\rho \in \mathbb{R}_+$ , on définit la boule ouverte de centre $x 0$ et de rayon $ρ$ comme étant l'ensemble définit par $\mathcal{B}(x_0,\rho):=\left\{x\in E\ /\ d(x,x_0)<\rho\right\}$ . La boule fermée de centre $x 0$ et de rayon $ρ$ est alors l'ensemble $\overline{\mathcal{B}}(x_0,\rho):=\left\{x\in E\ /\ d(x,x_0)\leq\rho\right\}$ (notation concordante avec la notion d'adhérence).
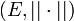
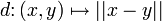
Dans un espace vectoriel normé $(E,||\cdot||)$ , on a la même définition en posant $d\colon(x,y)\mapsto||x-y||$ .

Exemples de boules exotiques

Si Z est muni de la distance induite par l'usuelle sur R, une boule ouverte de rayon 1 ne comporte qu'un point, le centre, et est aussi fermée tandis qu'une boule fermée de rayon 1 comporte trois points, et a pour intérieur la boule ouverte correspondante.
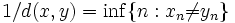
Si la distance d est ultramétrique, les boules sont à la fois ouvertes et fermées, tout point d'une boule en est un centre, et si deux boules se rencontrent l'une est contenue dans l'autre. On rencontre des distances ultramétriques en analyse p-adique mais aussi dans des situations plus élémentaires : sur l'ensemble des suites d'entiers N^N la distance naturelle d, définie par $1/d(x,y)=\inf\{n:x_n \not= y_n\}$ entre deux éléments x=(x_n) et y=(y_n) distincts de N^N, est ultramétrique et induit la topologie produit habituelle sur N^N.

Boules d'espaces normés

Par translation et homothétie, toutes les boules de rayon non nul sont semblables à la boule, ouverte ou fermée selon le cas, de centre l'origine et de rayon 1, appelée boule unité. Une boule unité est toujours un convexe non aplati symétrique par rapport à l'origine. D'après un théorème célèbre de F. Riesz, un espace vectoriel normé est de dimension finie si et seulement si sa boule (fermée) unité est compacte.

Sur un espace vectoriel de dimension finie sur R ou C, toutes les normes sont équivalentes. Cependant la forme géométrique des boules est diverse parmi les convexes symétriques. Par exemple, dans Rⁿ, toute partie convexe fermée, bornée, symétrique par rapport à l'origine et non aplatie est la boule fermée unité d'une certaine norme.

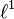
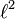
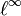
Sur Rⁿ (ou Cⁿ), il existe trois normes très usitées, dites norme $\ell^1$ , norme $\ell^2$ (c'est la norme euclidienne usuelle) et norme $\ell^{\infty}$ . Elles sont définies comme suit, pour x=(x₁,...,x_n) dans Rⁿ,

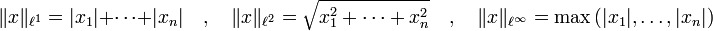
$\|x\|_{\ell^1}=|x_1|+\cdots+|x_n|\quad,\quad\|x\|_{\ell^2}=\sqrt{x_1^2+\cdots+x_n^2}\quad,\quad\|x\|_{\ell^{\infty}}=\max{(|x_1|,\dots,|x_n|)}$

Pour n=2, la boule unité de la première est un carré " en losange " inscrit dans la boule de la deuxième, un disque, lui-même inscrit dans la boule de la troisième, un carré " normal ".