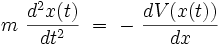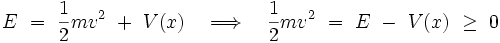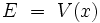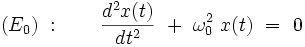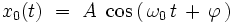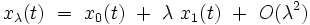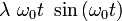Théorie des perturbations - Définition
La liste des auteurs de cet article est disponible ici.
Un deuxième exemple : l'oscillateur de Duffing
Définition et propriétés
Définition
L'oscillateur de Duffing satisfait à l'équation différentielle du second ordre suivante :
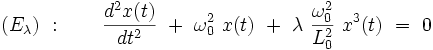
|
Dans cette équation, t représente le temps, ω0 un paramètre fixé homogène à une pulsation, c’est-à-dire l'inverse d'un temps. L0 est un paramètre fixé homogène à une longueur, et λ le paramètre de perturbation, sans dimensions. On cherche à déterminer la fonction x(t) inconnue, homogène à une longueur, et vérifiant les conditions initiales : à l'instant t = 0, on a : x(0) = X0 et
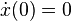
Interprétation physique
On peut interpréter cette équation différentielle comme la loi de la dynamique de Newton d'une particule de masse m soumise à une force dérivant d'une énergie potentielle V(x) :
|
|
où le potentiel V(x) quartique s'écrit :
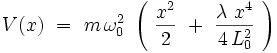
|
Caractère borné du mouvement
Pour toutes les valeurs de λ positives ou nulles, V(x) représente un puits de potentiel. La conservation de l'énergie mécanique totale E de la particule :
|
|
entraine alors que le mouvement est borné dans un intervalle
![[ \, x_1, \, x_2 \, ]](https://static.techno-science.net/illustration/Definitions/autres/6/67ad3f6577fc6223cabaa626311bee4c_411b39e44043192d441b2bb876e7da84.png)
|
|
Ordre zéro : l'oscillateur harmonique
Le problème de départ de la théorie des perturbations est l'équation différentielle (E0) correspondant à la valeur λ = 0 :
|
|
Cette équation est par définition un oscillateur harmonique de pulsation ω0, dont la solution analytique exacte est bien connue :
|
|
où A et

Théorie de perturbation naïve au premier ordre
On cherche la solution approchée sous la forme :
|
|
où x1(t) est une fonction inconnue, à déterminer. On injecte cette expression dans l'équation différentielle exacte (Eλ). En se limitant au termes du premier ordre inclus et en utilisant le fait que x0(t) est la solution exacte de (E0), on obtient l'expression au premier ordre de la théorie de perturbation :
![x_{\lambda}(t) \ = \ X_0 \ \cos \left( \omega_0 t \right) \ + \ \lambda \ \left[ \frac{X_0^3}{32 \, L_0^2} \left[ \, \cos \left( 3 \omega_0 t \right) \, - \, \cos \left( \omega_0 t \right) \, \right] \ + \ \frac{3 \, X_0^3}{8 \, L_0^2} \ \omega_0 t \ \sin \left( \omega_0 t \right) \ \right] \ + \ O(\lambda^2)](https://static.techno-science.net/illustration/Definitions/autres/f/f3eaccc49a1b0d8bf5cc5c86e785ce10_ef8336342c07948b58f6539a5ceaf6a8.png)
|
On injecte le développement dans l'équation différentielle exacte (Eλ). En se limitant au termes du premier ordre inclus et en utilisant le fait que x0(t) est la solution exacte de (E0), on obtient l'équation suivante pour la fonction x1(t) :
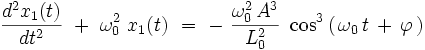
On utilise l'identité trigonométrique suivante :
![\cos^3 \alpha \ = \ \frac{1}{4} \ \left[ \ 3 \ \cos \alpha \ + \ \cos (3 \alpha ) \ \right]](https://static.techno-science.net/illustration/Definitions/autres/5/5b2a184929fbf0a772ceea144ec7919f_9060e9bd6e3b94cb02ce1cae8dfad1d5.png)
d'où l'équation différentielle pour la fonction x1(t) :
![\frac{d^2x_1(t)}{dt^2} \ + \ \omega_0^2 \ x_1(t) \ = \ - \ \frac{\omega_0^2 \, A^3}{4 \, L_0^2} \ \left[ \ 3 \ \cos \left( \, \omega_0 \, t \, + \, \varphi \, \right) \ + \ \cos \left( \, 3 \, \omega_0 \, t \, + \, 3 \, \varphi \, \right) \ \right]](https://static.techno-science.net/illustration/Definitions/autres/3/3de9fc20efeb35f92b712418ff9cf150_5603cfd206dfa569e23a5d0d4a929c91.png)
On peut démontrer que cette équation différentielle possède la solution générale exacte suivante :
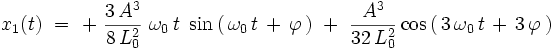
On a donc pour la fonction inconnue :
![x_{\lambda}(t) \ = \ A \ \cos \left( \, \omega_0 \, t \, + \, \varphi \, \right) \ + \ \lambda \ \left[ \, + \, \frac{3 \, A^3}{8 \, L_0^2} \ \omega_0 \, t \ \sin \left( \, \omega_0 \, t \, + \, \varphi \, \right) \ + \ \frac{A^3}{32 \, L_0^2} \cos \left( \, 3 \, \omega_0 \, t \, + \, 3 \, \varphi \, \right) \, \right] \ + \ O(\lambda^2)](https://static.techno-science.net/illustration/Definitions/autres/0/0ab874c5483abc620ed7c88af71a6e98_6bbb2057e0b55ccbf5406f627abee8b3.png)
L'application des conditions initiales : à l'instant t = 0, on a : x(0) = X0 et
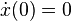
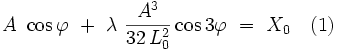
![- \ A \ \omega_0 \ \sin \varphi \ + \ \lambda \ \left[ \ \frac{3 \, \omega_0 \, A^3}{8 \, L_0^2} \ \sin \varphi \ - \ \frac{3 \omega_0 \, A^3}{32 \, L_0^2} \ \ \sin 3 \varphi \ \right] \ = \ 0 \quad (2)](https://static.techno-science.net/illustration/Definitions/autres/6/6e6e85c0fe9609081aefd5bbee1f4f7a_66e69120607fc11c88aefc492250913f.png)
En utilisant la formule trigonométrique :
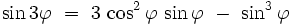
dans l'équation (2), on montre que :
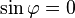
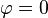
![A \ + \ \lambda \ \frac{A^3}{32 \, L_0^2} \ = \ X_0 \quad \Longrightarrow \quad A \ = \ X_0 \ \left[ \, 1 \, - \, \frac{\lambda \, X_0^2}{32 \, L_0^2} \, \right] \ + \ O(\lambda^2)](https://static.techno-science.net/illustration/Definitions/autres/8/806118cce2f2402e56e36fd80e354145_b3b05416e52c0b5a5b087e6882f74f15.png)
Apparition d'un terme séculaire
On constate que la perturbation contient un terme proportionnel au temps :
|
|
Ce terme non borné est appelé terme séculaire, du mot latin saeculum qui signifie siècle. En effet, pour les temps
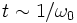
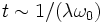
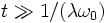
Dans le cadre de l'astronomie, la présence de ces termes séculaires empêchent d'étudier le futur à long terme des trajectoires planétaires, l'unité de temps caractéristique du problème étant le siècle.