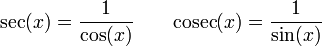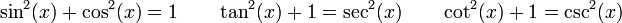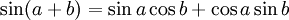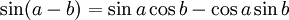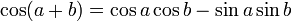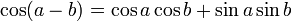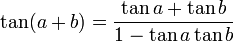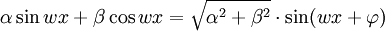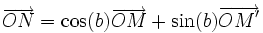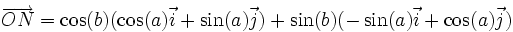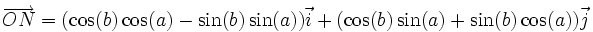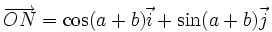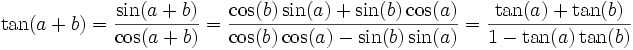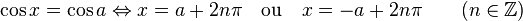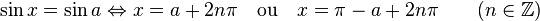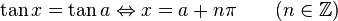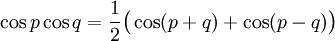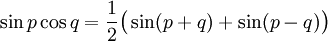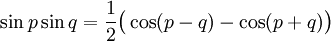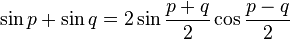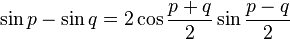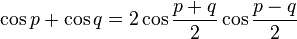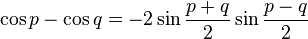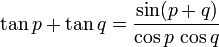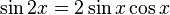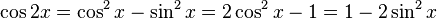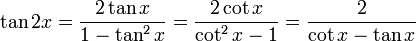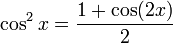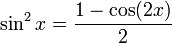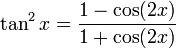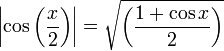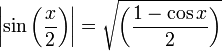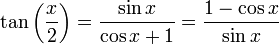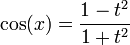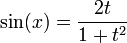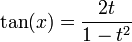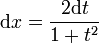Mercredi 11 Décembre 2024
Rechercher 🔍

Identité trigonométrique - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - À partir des définitions - À partir du théorème de Pythagore - Propriétés liées au cercle trigonométrique - Formules d'addition et de différence - Équation trigonométrique - Formules de Simpson - Formules de duplication et d'angle moitié - Formule de Moivre et formules d'angle multiple - Formules d'Euler - Fonctions trigonométriques réciproques - Linéarisation - Identités sans variable - Propriétés métriques dans un triangle quelconque - En analyse

Introduction

Une identité trigonométrique est une relation impliquant des fonctions trigonométriques et qui est vérifiée pour toutes les valeurs des variables intervenant dans la relation. Ces identités peuvent être utiles quand une expression comportant des fonctions trigonométriques a besoin d'être simplifiée. Elles constituent donc une « boîte à outils » utile pour la résolution de problèmes.

Les fonctions trigonométriques servent beaucoup en intégration, pour intégrer des fonctions « non trigonométriques » : un procédé habituel consiste à effectuer un changement de variable en utilisant une fonction trigonométrique, et à simplifier ensuite l'intégrale obtenue avec les identités trigonométriques.

Notation : avec les fonctions trigonométriques, nous définirons sin2, cos2, etc., les fonctions telles que pour tout réel x, sin2(x) = (sin(x))2, ...

À partir des définitions

\tan (x) = \frac {\sin (x)} {\cos(x)} \qquad \operatorname{cotan}(x) = \frac{1} {\tan (x)} = \frac {\cos (x)} {\sin(x)}
\operatorname{sec}(x) = \frac{1} {\cos(x)} \qquad \operatorname{cosec}(x) = \frac{1} {\sin(x)}

À partir du théorème de Pythagore

\sin^2(x) + \cos^2(x) = 1 \qquad \tan^2(x) + 1 = \sec^2(x) \qquad \cot^2(x) + 1 = \csc^2(x)

Propriétés liées au cercle trigonométrique

Symétries, parité

Parité - Réflexion d'axe θ = 0 Réflexion d'axe θ = π / 4 Réflexion d'axe θ = π / 2
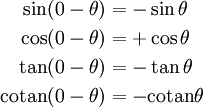
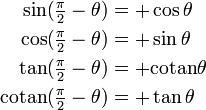
\begin{align} \sin(0 -\theta) &= -\sin \theta \\ \cos(0 -\theta) &= +\cos \theta \\ \tan(0 -\theta) &= -\tan \theta \\ \mathrm{cotan} (0 -\theta) &= -\mathrm{cotan} \theta \end{align} \begin{align} \sin(\tfrac{\pi}{2} - \theta) &= +\cos \theta \\ \cos(\tfrac{\pi}{2} - \theta) &= +\sin \theta \\ \tan(\tfrac{\pi}{2} - \theta) &= +\mathrm{cotan} \theta \\ \mathrm{cotan}(\tfrac{\pi}{2} - \theta) &= +\tan \theta \end{align}

Périodicité, décalages

Décalage de \dfrac{\pi}{2} Décalage de π
(Période de tan et cotan)		 Décalage de 2π
(Période de sin et cos)
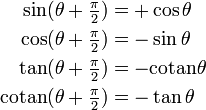
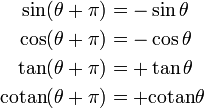
\begin{align} \sin(\theta + \tfrac{\pi}{2}) &= +\cos \theta \\ \cos(\theta + \tfrac{\pi}{2}) &= -\sin \theta \\ \tan(\theta + \tfrac{\pi}{2}) &= -\mathrm{cotan} \theta \\ \mathrm{cotan}(\theta + \tfrac{\pi}{2}) &= -\tan \theta \end{align} \begin{align} \sin(\theta + \pi) &= -\sin \theta \\ \cos(\theta + \pi) &= -\cos \theta \\ \tan(\theta + \pi) &= +\tan \theta \\ \mathrm{cotan}(\theta + \pi) &= +\mathrm{cotan} \theta \\ \end{align} \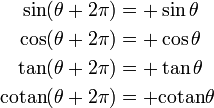begin{align} \sin(\theta + 2\pi) &= +\sin \theta \\ \cos(\theta + 2\pi) &= +\cos \theta \\ \tan(\theta + 2\pi) &= +\tan \theta \\ \mathrm{cotan}(\theta + 2\pi) &= +\mathrm{cotan} \theta \end{align}

Formules d'addition et de différence

Le moyen le plus rapide pour retrouver ces formules est d'utiliser les formules d'Euler en analyse complexe.

\sin (a + b) = \sin a \cos b + \cos a \sin b \,
\sin (a - b) = \sin a \cos b - \cos a \sin b \,
\cos (a + b) = \cos a \cos b - \sin a \sin b \,
\cos (a - b) = \cos a \cos b + \sin a \sin b \,

Un moyen mnémotechnique pour retenir : « Le cosinus est méchant (asocial et contestataire !) : il ne sympathise pas avec les sinus, et de plus il change les signes ».

\tan (a + b) = \frac{\tan a + \tan b}{1 - \tan a \tan b} \,

Une conséquence intéressante de ces égalités est qu'elles permettent de ramener la combinaison linéaire d'un sinus et d'un cosinus à un sinus :

\alpha\sin wx+\beta\cos wx=\sqrt{\alpha^2+\beta^2}\cdot\sin(wx+\varphi)

où

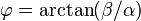
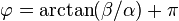
\varphi={\rm arctan}(\beta/\alpha) si α est positif et \varphi={\rm arctan}(\beta/\alpha) + \pi sinon

Il existe de nombreuses démonstrations possibles dont une utilisant les propriétés d'une corde dans un cercle et une autre la relation entre cosinus d'un angle et produit scalaire. La démonstration proposée ici démontre à la fois la formule du cosinus et celle du sinus. Elle utilise la propriété du changement de repère.

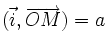
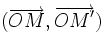
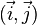
Sur le cercle trigonométrique, on considère le point M tel que (\vec i, \overrightarrow{OM}) = a et le point M' tel que la base (\overrightarrow{OM}, \overrightarrow{OM'}) soit orthonormale directe. Les deux vecteurs ont alors, dans la base (\vec i, \vec j) respectivement les coordonnées (cos(a),sin(a)) et ( − sin(a),cos(a))

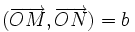
On considère le point N tel que ( \overrightarrow{OM}, \overrightarrow{ON}) = b .

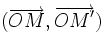
Dans la base (\overrightarrow{OM}, \overrightarrow{OM'}) , le vecteur \overrightarrow{ON} a pour coordonnées (cos(b);sin(b)). Ce qui conduit aux égalités vectorielles :

\overrightarrow{ON} = \cos(b)\overrightarrow{OM}+ \sin(b)\overrightarrow{OM'}
\overrightarrow{ON} = \cos(b)(\cos(a) \vec i + \sin(a) \vec j) + \sin(b)(-\sin(a)\vec i + \cos(a) \vec j)
\overrightarrow{ON} = (\cos(b)\cos(a) - \sin(b)\sin(a)) \vec i + (\cos(b)\sin(a) + \sin(b)\cos(a)) \vec j

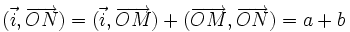
D'autre part, puisque (\vec i, \overrightarrow{ON}) = (\vec i, \overrightarrow{OM}) + (\overrightarrow{OM},\overrightarrow{ON}) = a + b , on a :

\overrightarrow{ON} = \cos(a+b) \vec i + \sin(a+b) \vec j

Les formules s'obtiennent alors par identification.

La formule de la tangente s'obtient alors par quotient

\tan(a+b) = \frac{\sin(a+b)}{\cos(a+b)} = \frac{\cos(b)\sin(a) + \sin(b)\cos(a)}{\cos(b)\cos(a) - \sin(b)\sin(a)} = \frac{\tan(a) + \tan(b)}{1 - \tan(a)\tan(b)}

par division au numérateur et dénominateur par cos(a)cos(b)

Équation trigonométrique

\cos x = \cos a \Leftrightarrow x=a+2n\pi \quad \text{ou} \quad x=-a+2n\pi \qquad(n\in\mathbb{Z})
\sin x = \sin a \Leftrightarrow x=a+2n\pi \quad \text{ou} \quad x=\pi-a+2n\pi \qquad(n\in\mathbb{Z})
\tan x = \tan a \Leftrightarrow x=a+n\pi \qquad(n\in\mathbb{Z})

Formules de Simpson

Transformation de produits en sommes

\cos p\cos q=\frac{1}{2}\bigl(\cos(p+q)+\cos(p-q)\bigr)
\sin p\cos q=\frac{1}{2}\bigl(\sin(p+q)+\sin(p-q)\bigr)
\sin p\sin q=\frac{1}{2}\bigl(\cos(p-q)-\cos(p+q)\bigr)

Ces formules peuvent être démontrées en développant leurs membres de droite en utilisant les formules d'addition

Transformation de sommes en produits

\sin p + \sin q = 2\sin\frac{p+q}{2}\cos\frac{p-q}{2}
\sin p - \sin q = 2\cos\frac{p+q}{2}\sin\frac{p-q}{2}
\cos p + \cos q = 2\cos\frac{p+q}{2}\cos\frac{p-q}{2}
\cos p - \cos q = -2\sin\frac{p+q}{2}\sin\frac{p-q}{2}

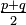
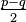
Il suffit de remplacer p par \tfrac{p+q}{2} et q par \tfrac{p-q}{2} dans les formules de transformation de produit en somme.

Un moyen mnémotechnique pour retenir : « Si, coco, si ; coco, si si ! Priorité au sinus et à l'addition, −2 à la dernière ».

\tan p + \tan q = \frac{\sin(p+q)}{\cos p\,\cos q}

Formules de duplication et d'angle moitié

Formules de l'angle double

Appelées aussi formules d'angle double, elle peuvent être obtenues en remplaçant a et b par x dans les formules d'addition et en utilisant le théorème de Pythagore pour les deux dernières, ou bien en utilisant la formule de Moivre avec n = 2.

\sin 2x = 2 \sin x\cos x\,
\cos 2x= \cos^2 x - \sin^2 x = 2 \cos^2 x-1 = 1-2 \sin^2 x \,
\tan 2x = \frac{2 \tan x}{1 - \tan^2 x} = \frac{2 \cot x}{\cot^2 x- 1} = \frac{2}{\cot x - \tan x}

Une conséquence amusante de la formule de duplication du cosinus est la suivante :

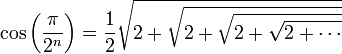
\cos\left(\frac{\pi}{2^n}\right)=\frac{1}{2}\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\cdots}}}} avec n-1 « 2 » sous le radical.

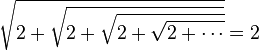
En passant à la limite, on a une démonstration du fait que \sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\cdots}}}}=2

Formules de réduction du carré

Ces formules permettent d'écrire cos2(x), sin2(x) et tan2(x) en fonction du cosinus de l'angle double.

\cos^2 x = \frac{1 + \cos(2x)}{2}
\sin^2 x = \frac{1 - \cos(2x)}{2}
\tan^2 x = \frac{1 - \cos(2x)}{1 + \cos(2x)}

Formules d'angle moitié

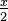
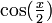
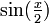
En remplaçant x par \tfrac{x}{2} dans les formules de réduction des carrés, et ensuite en cherchant l'expression de \cos(\tfrac x2) et \sin(\tfrac x2) , nous obtenons :

\left|\cos\left(\frac{x}{2}\right)\right| = \sqrt{\left(\frac{1 + \cos x}{2}\right)}
\left|\sin\left(\frac{x}{2}\right)\right| = \sqrt{\left(\frac{1 - \cos x}{2}\right)}

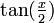
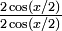
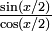
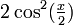
En multipliant \tan(\tfrac x2) par \tfrac{2\cos(x/2)}{2\cos(x/2)} et en le remplaçant par \tfrac{\sin(x/2)}{\cos(x/2)} on obtient au numérateur sinx d'après la formule d'angle double, et au dénominateur 2\cos^2(\tfrac x2) qui est aussi égal à cosx + 1 selon la formule de réduction du carré.

La seconde formule vient de la première en multipliant numérateur et dénominateur par sinx et en simplifiant en utilisant le théorème de Pythagore et l'identité remarquable 1 − cos2x = (1 − cosx)(1 + cosx).

\tan\left(\frac{x}{2}\right) = \frac{\sin x}{\cos x + 1} = \frac{1 - \cos x}{\sin x}

Formules impliquant la « tangente de l'arc moitié »

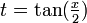
Si on pose t=\tan(\tfrac{x}{2}) , on a :

\cos(x)=\frac{1-t^2}{1+t^2}
\sin(x)=\frac{2t}{1+t^2}
\tan(x)=\frac{2t}{1-t^2}

Dans le cas de changement de variable en intégration, on ajoutera :

\mathrm d x = \frac{2\mathrm d t}{1 + t^2}

Ces formules permettent de simplifier des calculs trigonométriques en se ramenant à des calculs sur des fractions rationnelles. Elles permettent aussi de déterminer l'ensemble des points rationnels du cercle unité.

Formule de Moivre et formules d'angle multiple
- Introduction - À partir des définitions - À partir du théorème de Pythagore - Propriétés liées au cercle trigonométrique - Formules d'addition et de différence - Équation trigonométrique - Formules de Simpson - Formules de duplication et d'angle moitié - Formule de Moivre et formules d'angle multiple - Formules d'Euler - Fonctions trigonométriques réciproques - Linéarisation - Identités sans variable - Propriétés métriques dans un triangle quelconque - En analyse
miniature
Le télescope James Webb, poussé à ses limites, découvre ces structures incroyablement anciennes 🔭
miniature
Le rôle surprenant de la grossesse contre la grippe A 🦠
miniature
Découverte d'une nouvelle espèce éteinte grâce à... un accélérateur de particules ⚛️
miniature
Une avancée prometteuse pour le déploiement des batteries sodium-ion 🔋
miniature
Voici comment et pourquoi le risque de cancer augmente... puis diminue avec l'âge 🧬
miniature
Le Soleil bientôt en "zone de combat": une période de turbulences extrêmes ☀️
miniature
1
Les rhumatismes plus douloureux par temps humide: vrai ou faux ? 🌧️
miniature
Ce nouveau type de moteur repousse les limites du vol supersonique ✈️
miniature
Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠
miniature
Une super-Terre entre Mars et Jupiter ? 🌎
miniature
Découverte impressionnante d'un fossile de crocodile géant 🐊
miniature
1
Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡
miniature
1
Un virage technologique révèle l'impact du diabète gestationnel 🩺
miniature
Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼
miniature
1
Ce fin gilet robotisé soulage les tâches répétitives 🦾
miniature
Les équations d'Einstein invalidées ? 👀
miniature
Ce tatouage électronique se connecte à votre cerveau 🧠
miniature
Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️
miniature
Des plats au bœuf... sans bœuf ? 🥩
miniature
2
Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍
miniature
Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️
miniature
Découverte: d'autres univers plus propices à la vie que le notre 👽
miniature
Ces sons urbains qui minent notre santé mentale 🚗
miniature
La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥
miniature
Des microalgues éliminent les métaux lourds: voici comment 🧪
miniature
1
Et voici un qubit mécanique ! 🖥️
miniature
Les lentilles de contact sont-elles vraiment sans danger ? 👁️
miniature
Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥
miniature
4
Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠
miniature
Cette astuce quotidienne ajoute 11 ans à votre vie 🕒
miniature
Révolutions, migrations des européens... les éruptions volcaniques ont influencé l'histoire 🌋
miniature
Soit l'énergie noire n'est pas constante, soit une seconde force inconnue est à l'œuvre... 🌀
miniature
Voici pourquoi l'alcool peut rendre agressif 🥂
miniature
Expérience inédite: ce laser projette une ombre visible 💥
miniature
Ce plat millénaire réduit significativement la graisse corporelle 🍽️
miniature
Les scientifiques trompés ? La Voie Lactée n'est PAS comme les autres galaxies 🔭
miniature
Pourquoi ce que pensent les autres de nous nous fait tant ruminer ? 🧠
miniature
De la vie découverte sur un échantillon de l'astéroïde Ryugu (oups) 👽
miniature
2
Des anomalies incompréhensibles de températures détectées simultanément presque partout sur Terre 🌡️
miniature
Cette planète, trop jeune pour exister, bouscule les lois de l'astronomie 🪐
miniature
Une montagne d'or découverte en Chine ⛏️
miniature
Cette simulation de l'Univers est totalement vertigineuse 🌀
miniature
1
Une pilule pourrait-elle imiter les bienfaits du yoga ? 🧘
miniature
Nous serions-nous trompés sur l'origine de l'écriture alphabétique ? ✍️
miniature
Voici pourquoi votre enfant triche et ce que cela révèle 🧠
miniature
Le Sahara verdit, et cela pourrait bien (re)changer notre climat 🌱
miniature
1
Neuralink: un bras robotique contrôlé par la pensée 🦾
miniature
Ces fossiles humains à grands crânes seraient-ils une espèce jusqu'alors inconnue ? 💀
miniature
1
L'étonnant impact du froid sur notre sommeil ❄️
miniature
Une base cachée de missiles nucléaires repérée par erreur sous la calotte glacière ☢️
Page générée en 0.245 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise