Théorie des perturbations - Définition
La liste des auteurs de cet article est disponible ici.
Un premier exemple élémentaire
Position du problème
Considérons à titre d'exemple l'équation différentielle du premier ordre suivante :
|
|
Dans cette équation, t représente le temps, τ un paramètre fixé homogène à un temps, L0 un paramètre fixé homogène à une longueur, et λ le paramètre de perturbation, sans dimensions. On cherche à déterminer la fonction x(t) inconnue, homogène à une longueur, et vérifiant la condition initiale : à l'instant t = 0, on a : x(0) = X0.
Théorie des perturbations au premier ordre
Le problème de départ de la théorie des perturbations est l'équation différentielle (E0) correspondant à la valeur λ = 0 :
|
|
dont la solution analytique exacte est bien connue :
|
|
où A est une constante, pour l'instant inconnue. Illustrons la méthode de perturbations en nous limitant pour simplifier au premier ordre dans le développement en série des puissances du paramètre λ ; on cherche donc la solution approchée sous la forme :
|
|
où x1(t) est une fonction inconnue, à déterminer. On injecte cette expression dans l'équation différentielle exacte (Eλ). En se limitant aux termes du premier ordre inclus et en utilisant le fait que x0(t) est la solution exacte de (E0), on obtient la solution physique approchée au premier ordre :
|
|
On injecte le développement dans l'équation différentielle exacte (Eλ). En se limitant au termes du premier ordre inclus et en utilisant le fait que x0(t) est la solution exacte de (E0), on obtient l'équation suivante pour la fonction x1(t) :
![\lambda \ \left[ \ \frac{dx_1(t)}{dt} \ + \ \frac{1}{\tau} \ x_1(t) \ \right] \ + \ \lambda \ \frac{x^2_0(t)}{\tau \, L_0} \ = \ 0](https://static.techno-science.net/illustration/Definitions/autres/4/4411e593eb03638b074d432a00c46974_1c7084715502f2e7087036a53b2d467f.png)
On a omis le terme O(λ2) de reste de Landau pour simplifier l'écriture. Cette équation se réécrit explicitement :
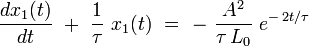
Cette équation différentielle admet une solution analytique exacte de la forme :
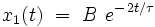
où B est une constante, qu'on détermine en introduisant l'expression de x1(t) dans l'équation différentielle. On obtient explicitement :
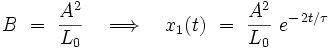
Comparaison avec la solution exacte
On peut démontrer ici que l'équation différentielle (Eλ) vérifiant la condition initiale : x(0) = X0 admet pour toutes les valeurs du paramètre λ la solution exacte suivante :
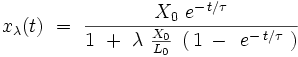
|
Un développement limité de cette expression au premier ordre en λ donne explicitement la solution approchée déterminée au paragraphe précédent par la théorie des perturbations au premier ordre :
|
|
Pour visualiser l'écart entre la solution approchée et la solution exacte, on trace ci-dessous les graphes des deux fonctions pour une série de valeurs de λ allant de 0.1 à 0.5, en prenant : X0 = L0 = 1 m, τ = 1 s.
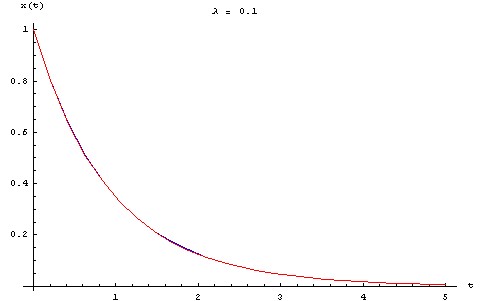
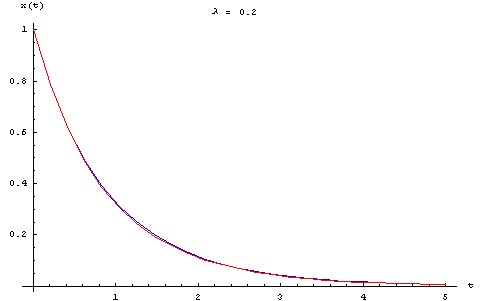
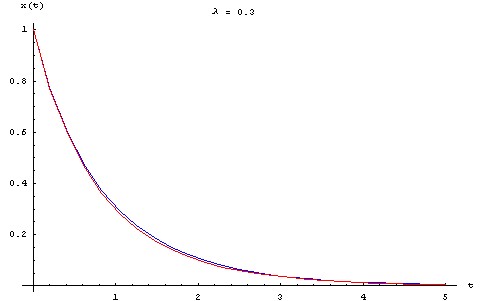
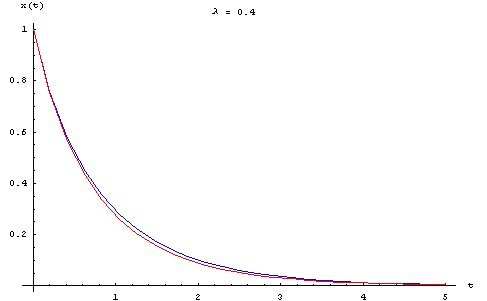
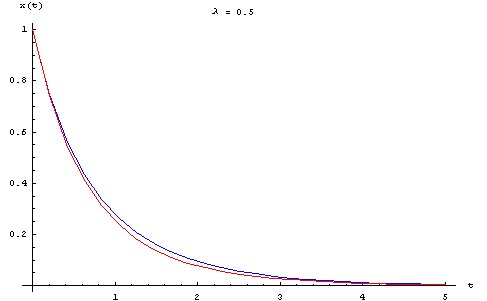
Perturbation singulière
Voir l'article Renormalisation
Méthode de Lindstedt
Lindstedt a proposé en 1882 une méthode qui, pour certaines équation différentielles, permet d'éliminer ces termes séculaire. On l'appelle aussi méthode de Lindstedt-Poincaré, Poincaré ayant démontré que les séries introduites par Lindstedt devaient être interprétées comme des expressions asymptotiques.
L'idée de Lindstedt est la suivante : dans certains cas, les termes séculaires peuvent être dus au fait que l'on développe incorrectement les expressions. Par exemple, supposons que le résultat exact soit :
|
|
Cette expression clairement bornée développée au premier ordre en λ donne :
|
|
et il apparait un terme séculaire non borné ! On voit que la solution exacte est en fait une fonction de la pulsation :
|
|
qui est légèrement différente de la pulsation initiale ω0 du problème. Lindstedt va utiliser cette remarque de façon systématique.
Principe de la méthode de Lindstedt
La méthode de Lindstedt ne s'applique que pour les équations différentielles du type suivant :
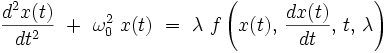
|
où f est une fonction paire de x et impaire de
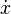
|
|
Dans cette expression, les valeurs numériques des constantes inconnues
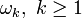
Illustrons la méthode dans le paragraphe suivant avec l'oscillateur de Duffing.
Exemple : l'oscillateur de Duffing au premier ordre
On a vu plus haut que l'équation différentielle de l'oscillateur de Duffing s'écrivait :
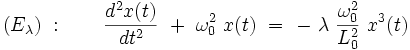
|
Faisons le changement d'échelle de temps
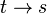
|
|
La règle de Leibniz de dérivation en chaine donne pour la dérivée première :
|
|
et pour la dérivée seconde :
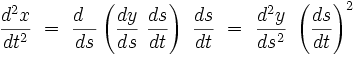
|
Comme on a au premier ordre :
|
|
on obtient pour les dérivées :
|
|
|
|
L'équation différentielle de Duffing devient au premier ordre :
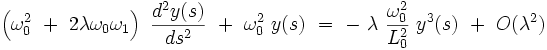
|
Introduisons maintenant dans cette équation différentielle le développement au premier ordre de la solution :
|
|
Il vient en développant selon les puissances de λ :
![\omega_0^2 \left(\frac{d^2y_0}{ds^2} + y_{0} \right) \ + \ \lambda \left[ \omega_0^2 \frac{d^2y_1}{ds^2} + 2 \omega_0 \omega_1 \frac{d^2y_0}{ds^2} + \omega_0^2 y_1 + \frac{\omega_0^2}{L_0^2} \ y_0^3 \right] \ = \ 0 + O(\lambda^2)](https://static.techno-science.net/illustration/Definitions/autres/4/4be2eba910fb3ebf97be3d0c08c81abb_65e31715808426f1918ad73a93ce1380.png)
|
On a donc le système de deux équations différentielle :
|
|
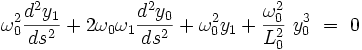
|
La première a pour solution générale :
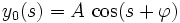

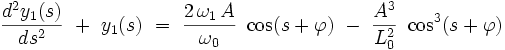
|
On réutilise la formule trigonométrique :
|
|
d'où l'équation différentielle pour la fonction y1(s) :
![\frac{d^2y_1(s)}{ds^2} \ + \ y_1(s) \ = \ \left[ \ \frac{2 \, \omega_1}{\omega_0} \ - \ \frac{3 \, A^3}{4L_0^2} \right] \ \cos (s + \varphi) \ - \ \frac{A^3}{4L_0^2} \ \cos (3s + 3 \varphi )](https://static.techno-science.net/illustration/Definitions/autres/b/b07e621a476d09ddc41b80eb3f51fa68_c02f871753c11946edcddfe142836e6e.png)
|
Il suffit alors d'annuler le coefficient devant le terme en
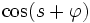
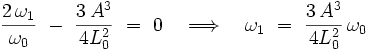
|
On obtient alors l'équation différentielle finale pour la fonction y1(s) :
Cette équation différentielle admet une solution générale bornée sans terme séculaire :
A suivre ...
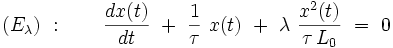
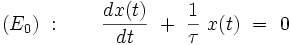
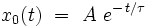
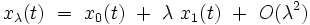
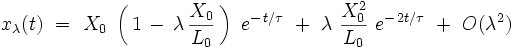
![x_{\lambda}(t) \ = \ X_0 \ \cos \left[ \, \left( 1 + \lambda \right) \, \omega_0 t \, \right]](https://static.techno-science.net/illustration/Definitions/autres/3/3e40f6e950e4d47ae12f67b8632b3c78_6dbd5b4da1d0d1938125f4ba42c6f053.png)
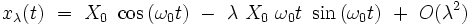
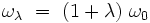
![s \ = \ \left[ \ \omega_0 \ + \ \lambda \omega_1 \ + \ \lambda^2 \omega_2 \ + \ \dots \ \right] \ t](https://static.techno-science.net/illustration/Definitions/autres/2/2e8d1def18d5e8e327e0db5c9cea5fd9_52b676fde937e49c3c7adae5aeb307ec.png)
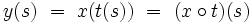
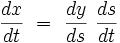
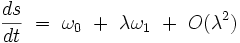
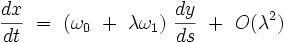
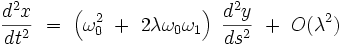
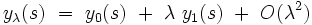
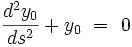
![\cos^3 \alpha \ = \ \frac{1}{4} \ \left[ \ 3 \ \cos \alpha \ + \ \cos (3 \alpha ) \ \right]](https://static.techno-science.net/illustration/Definitions/autres/5/5b2a184929fbf0a772ceea144ec7919f_9060e9bd6e3b94cb02ce1cae8dfad1d5.png)

















































