Renormalisation - Définition

Introduction

En théorie quantique des champs (ou QFT), en mécanique statistique des champs, dans la théorie des structures géométriques autosimilaires, une renormalisation se rapporte à un ensemble de techniques utilisées pour prendre la limite du continu.

Quand on décrit l'espace et le temps comme un continuum, certaines constructions statistiques et quantiques deviennent indéfinies. Pour les définir, il faut prendre des précautions pour passer à la limite.

La renormalisation détermine la façon de relier les paramètres de la théorie quand ces paramètres à grande échelle diffèrent de leur valeur à petite échelle. La renormalisation a été initialement développée en électrodynamique quantique (QED), en vue d'interpréter des intégrales divergentes de la théorie des perturbations. Au début, elle est considérée comme une procédure suspecte et provisoire par certains de ses auteurs. Finalement la renormalisation a été incorporée comme un outil important et logiquement cohérent dans plusieurs domaines de physique et de mathématiques.

L'idée majeure de la renormalisation est de corriger le lagrangien original d'une théorie quantique des champs par une série infinie de contre-termes, correspondant aux graphes de Feynman qui codent le développement perturbatif de la théorie. Dans la procédure de renormalisation perturbative, on introduit un contre-terme dans le lagrangien initial pour chaque divergence de graphe de Feynman. Dans certains cas, tous les contre-termes nécessaires peuvent être obtenus par modification des seuls paramètres du lagrangien initial. Il est alors possible de modifier ces paramètres, en les remplaçant par des séries de contre-termes divergents. Les paramètres initiaux ne sont pas observables, par opposition aux quantités physiques, qui sont finies, et observables. Un des problèmes de la procédure de renormalisation est le traitement systématique dans les graphes à plusieurs boucles des divergences liées à des boucles croisées ou incluses les unes dans les autres.

Auto-interactions en physique classique

Le problème des divergences est apparu tout d'abord en électrodynamique classique des particules ponctuelles aux et début du XX^e siècles.

La masse d'une particule chargée doit inclure la masse-énergie de son champ électrostatique. Supposons que la particule soit une sphère chargée de rayon r_e. L'énergie de ce champ est, en posant c=1 et ε₀=1 :

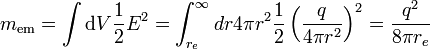
et elle devient infinie quand r_e → 0 , ce qui est évidemment absurde (puisque cela impliquerait que la particule ponctuelle ne pourrait pas être accélérée, en raison de sa masse infinie.

En passant, la valeur de r_e qui rend m_em égal à la masse de l'électron est appelée le rayon classique de l'électron, et se trouve α fois la longueur d'onde de Compton de l'électron. En remettant tous les multiples de c et de ε₀, on peut écrire :

Fig. 1 ─ Renormalisation en QED : la simple interaction électron-photon qui définit la charge de l'électron à un point de renormalisation se révèle à un autre point composée de plusieurs interactions plus compliquées.

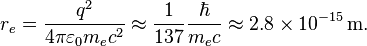
La masse totale effective d'une particule chargée sphérique inclut – outre la masse calculée supra pour le champ électromagnétique – la masse nue de la particule chargée. Si on permet à cette dernière d'être négative, on peut envisager d'un passage cohérent à la limite ponctuelle. Ceci a été appelé renormalisation. Lorentz et (en) Abraham ont essayé de cette manière de mettre au point une théorie classique de l'électron. Ces travaux précoces ont inspiré des essais ultérieurs de régularisation en physique et la renormalisation en QFT.

Quand on calcule les interactions électromagnétiques de particules chargées, il est tentant d'ignorer la rétroaction du champ d'une particule sur elle-même. Mais cette rétroaction est nécessaire pour expliquer le ralentissement de particules chargées qui rayonnent. Si l'on suppose l'électron ponctuel, la valeur de la rétroaction diverge, pour la même raison que la masse diverge, parce que le champ se comporte comme le carré inverse de la distance.

La théorie d'Abraham et Lorentz impliquait une « préaccélération » non causale. Dans certaines configurations, un électron commençait à se déplacer avant que la force ne soit appliquée. Ceci signalait que la limite ponctuelle n'était pas cohérente. Un corps étendu ne commencera à bouger que quand une force est appliquée sur un point au plus à sa surface.

Le problème s'est trouvé pire en théorie classique des champs qu'en QFT, parce que dans cette dernière, à courte distance, une particule se trouve dans une position fluctuante, et on ne peut donc la localiser mieux que dans une région de l'ordre de la longueur d'onde de Compton. En QED, à faible couplage, la masse électromagnétique ne diverge que comme le logarithme du rayon de la particule.

Certains physiciens pensent que quand la constante de structure fine est bien plus grande que l'unité, si bien que le rayon classique de l'électron est supérieur à la longueur d'onde de Compton, certains problèmes qui rendent la théorie classique incohérente reviennent en théorie quantique. En effet les problèmes de la théorie classique apparaissent à des distances de l'ordre du rayon classique, mais ils sont dilués par le principe d'incertitude sur une échelle plus grande, celle de la longueur d'onde de Compton. Si la constante de structure fine est plus grande que l'unité, alors c'est la situation inverse qui prévaut : les problèmes de la théorie classique peuvent se manifester avant d'être dilués par les fluctuations quantiques.