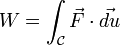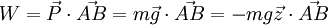Travail d'une force - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le travail d'une force est l'énergie fournie par cette force lorsque son point d'application se déplace (l'objet subissant la force se déplace ou se déforme). Si par exemple on pousse une voiture, le travail de la poussée est l'énergie produite par cette poussée. Cette notion avec ce nom fut introduite par Gaspard-Gustave Coriolis. Le travail est exprimé en joules (J), et est souvent noté W, initiale du mot anglais Work qui signifie travail.
Définition
Une force constante


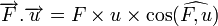
On remarque que seule la composante de


Si la force change au cours du trajet, ou si le trajet n'est pas rectiligne, on se ramène à une courte durée dt pendant laquelle la force peut être supposée constante et le trajet parcouru
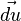
-
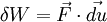
On peut alors obtenir le travail total fourni par la force

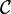

Si la trajectoire est circulaire (par exemple dans le cas où le point d'application d'une force est en rotation autour d'un axe
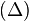
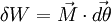
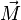
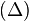
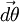
Travail des forces conservatives : exemple du poids
Les forces conservatives sont, par définition, des forces dont le travail ne dépend pas du chemin suivi. Le poids en est un exemple.
Considérons un corps de masse m se déplaçant de A vers B dans un repère galiléen
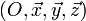
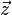
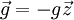
Si l'on note
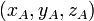
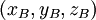
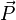
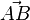
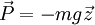
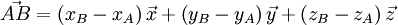
et, par définition du produit scalaire, le travail du poids se simplifie de la façon suivante :
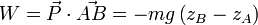
Le travail du poids d'un corps est donc indépendant du chemin suivi lors de son déplacement, il ne dépend que de la variation d'altitude du centre de gravité de ce corps.
Exemple de calcul
Une personne de masse 80 kg monte debout sur une chaise de 50 centimètres de haut. Quel est le travail effectué par le poids de cette personne ?
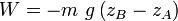
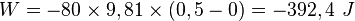
Où 9,81 représente la constante g caractéristique de la Terre (en newton par kilogramme), 80 la masse en kilogramme et 0,5 la hauteur en mètre.
Le poids est une force résistante dans ce cas (Il « s'oppose » au déplacement de la personne).
Cas concrets
Considérons une force

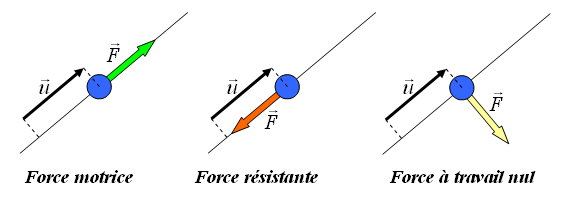
- Si la force


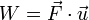
- Si
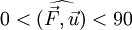
 le travail fourni par la force est positif.
le travail fourni par la force est positif.
La force est motrice.-
- On peut dire plus simplement que si la force

- On peut dire plus simplement que si la force
-
- Si la force


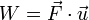
- Si
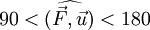
 le travail fourni par la force est négatif.
le travail fourni par la force est négatif.
La force est résistante.-
- On peut dire plus simplement que si la force

- On peut dire plus simplement que si la force
-
- Si la force


-
- On peut dire plus simplement que si la force

- On peut dire plus simplement que si la force
-
Ce dernier cas ne doit pas laisser penser qu'une force dont le travail est nul n'a aucun effet sur un système. Ainsi, dans le cas d'un solide en mouvement circulaire uniforme, la force centripète a un travail nul (le mouvement circulaire uniforme n'est pas modifié). Pour autant, si l'on supprime la force centripète le solide cessera son mouvement circulaire et se déplacera en mouvement rectiligne, conformément à la 1ère loi de Newton.
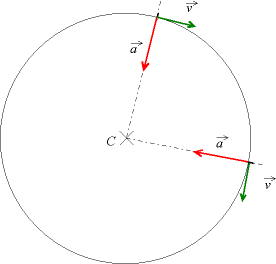
Les forces dont le travail est nul ne modifient pas l'énergie cinétique du solide. En particulier, elles ne modifient pas la norme de la vitesse ; elles peuvent cependant en modifier la direction.