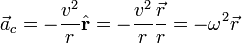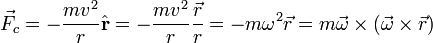Force centripète - Définition

Introduction

Une balle accrochée par un fil tourne autour d'un axe. La force centripète est exercée par le fil sur la balle pour la maintenir en rotation sur la trajectoire spécifiée. C'est cette force qui donne au fil sa tension.

Le terme force centripète ("qui tend à rapprocher du centre", en latin) désigne une force permettant de maintenir un objet dans une trajectoire circulaire ou, plus généralement, elliptique. En effet, tout objet décrivant une trajectoire elliptique possède en coordonnées cylindriques une accélération radiale non nulle, appelée accélération centripète, qui est dirigée vers le centre de courbure. D'un point de vue dynamique, le Principe Fondamental (PFD) indique alors la présence d'une force radiale dirigée elle aussi vers le centre de courbure.

Cette force est au sens de Newton une force réelle, qui pourra avoir diverses origines, par exemple :

• force de gravitation (mouvement des planètes)

• force de tension (mouvement circulaire d'une masse accrochée à un fil tendu dont l'autre extrémité est généralement fixe (ou quasiment))

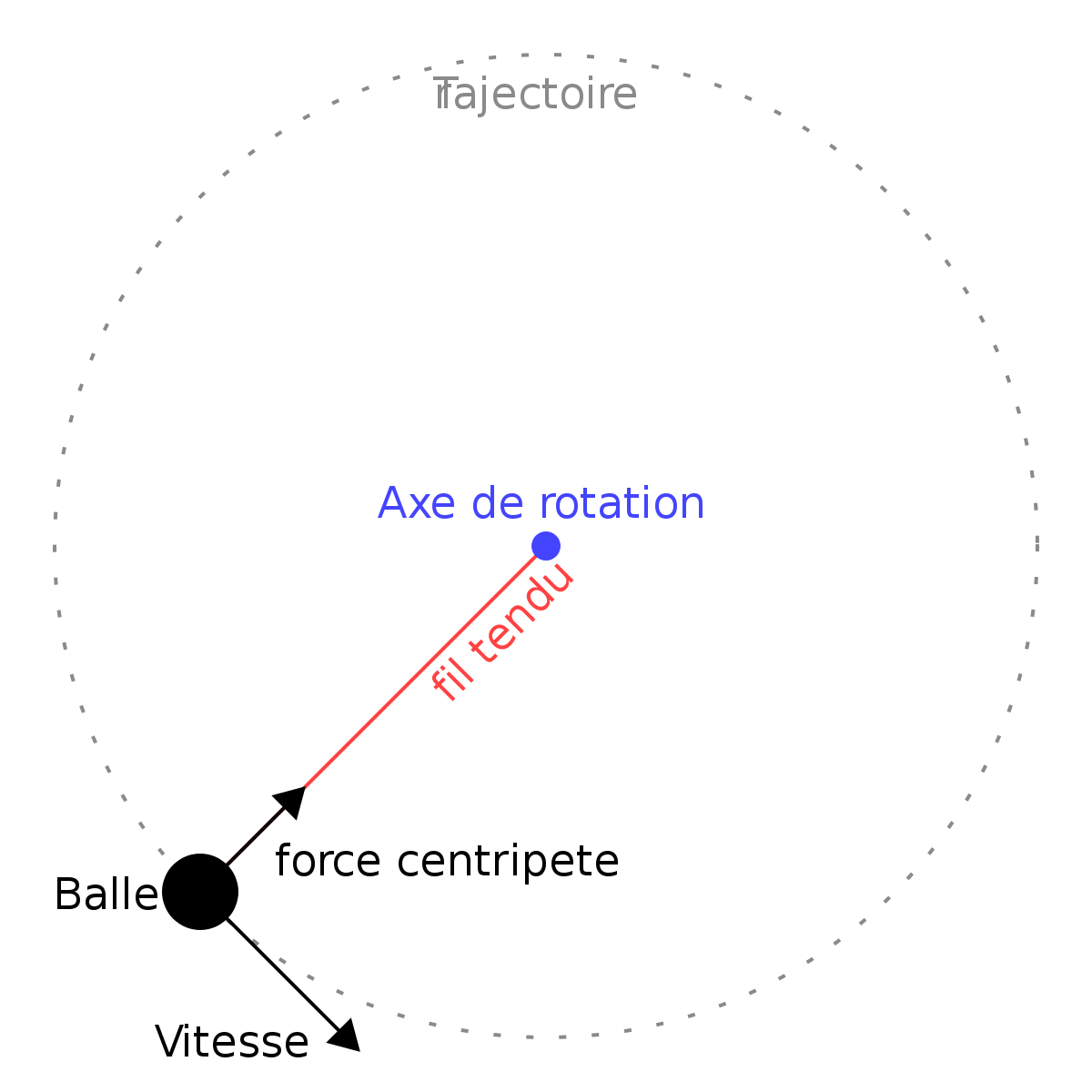
Sans force centripète, l'objet ne peut pas tourner ou cesse de tourner. Dans l'illustration ci-contre, si le fil casse, la balle cesse de tourner et poursuit par simple inertie un mouvement rectiligne, tangent à son ancienne trajectoire circulaire. Ce point de vue est celui d'un observateur situé en dehors du dispositif tournant (comme le lecteur qui regarde le schéma - ce repère est galiléen). Pour un observateur situé au centre de rotation et tournant avec lui (le repère est alors non galiléen) l'éjection de la balle est perçue différemment, comme l'effet d'une force dite force centrifuge (la force centrifuge est dite fictive car elle n'intervient que dans le repère en rotation, pour interpréter un effet subjectif).

Dans un référentiel galiléen un corps isolé possède, s'il est en mouvement, une trajectoire rectiligne uniforme (vitesse constante). Lui faire parcourir une trajectoire elliptique revient le dévier constamment, et donc à lui appliquer à tout instant une force dirigée vers le centre de courbure. Cette force est alors qualifiée de centripète. Le caractère centripète d'une force n'est pas intrinsèque, mais lui est conféré par son effet sur la trajectoire de l'objet. Il serait plus correct de parler de force à effet centripète.

Par construction, la force centripète est radiale, dirigée vers le centre de courbure, et son intensité est inversement proportionnelle au rayon de courbure de la trajectoire du point d'application.

Formule de base

Le vecteur vitesse est défini par la vitesse et la direction du mouvement. Si la résultante (c'est-à-dire la somme des vecteurs) des forces appliquées à un objet est nulle, cet objet n'accélère pas et donc se déplace sur une ligne droite à vitesse constante : le vecteur vitesse est constant. Par contre, un objet qui se déplace à vitesse constante et dont la trajectoire est un cercle change en permanence de direction de mouvement. Le taux de variation du vecteur vitesse est alors appelé accélération centripète.

Cette accélération centripète dépend du rayon r du cercle et de la vitesse v de l'objet. Plus la vitesse est grande, plus l'accélération augmente, de même plus le rayon est petit, plus elle augmente. De manière plus précise, l'accélération centripète est donnée par la formule

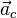
où ω = v / r est la vitesse angulaire. Le signe négatif indique que la direction de cette accélération est dirigée vers le centre du cercle, c'est-à-dire opposée au vecteur position . (On suppose que l'origine de est placée au centre du cercle.) désigne le vecteur unitaire dans la direction de .

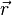
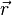
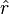
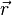
D'après la Seconde loi de Newton, , la force physique doit être appliquée à une masse m pour produire une telle accélération. La quantité de force nécessaire pour se déplacer à la vitesse v sur le cercle de rayon r est:

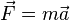
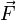
l'expression ayant été formulée de différentes manières équivalentes. Ici, est le vecteur de vitesse angulaire. Ici encore, le signe négatif indique que la direction est dirigée vers l'intérieur vers le centre du cercle et dans la direction opposée au vecteur rayon . Si la force appliquée est moins forte respectivement plus forte que , l'objet va glisser vers l'extérieur respectivement l'intérieur, se déplaçant sur un cercle plus grand, resp. plus petit.

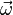
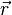
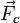
Si un objet se déplace sur un cercle à une vitesse variable, son accélération peut être divisée en deux composantes : l'accélération radiale (l'accélération centripète) qui change la direction de la vitesse et une composante tangentielle qui change l'amplitude de la vitesse.