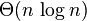Tri par insertion - Définition

Introduction

Exemple du tri par insertion utilisant une liste de nombres aléatoires

Le tri par insertion est un algorithme de tri classique dont le principe est très simple. C'est le tri que la plupart des personnes utilisent naturellement pour trier des cartes : prendre les cartes mélangées une à une sur la table, et former une main en insérant chaque carte à sa place.

En général, le tri par insertion est beaucoup plus lent que d'autres algorithmes comme le tri rapide et le tri fusion pour traiter de grandes séquences, car sa complexité asymptotique est quadratique.

Le tri par insertion est cependant considéré comme le tri le plus efficace sur des entrées de petite taille. Il est aussi très rapide lorsque les données sont déjà presque triées. Pour ces raisons, il est utilisé en pratique en combinaison avec d'autres méthodes comme le tri rapide (ou quicksort).

En programmation informatique, on applique le plus souvent ce tri à des tableaux. La description et l'étude de l'algorithme qui suivent se restreignent à cette version, tandis que l'adaptation à des listes est considérée plus loin.

Description de l'algorithme

Dans l'algorithme, on parcourt le tableau à trier du début à la fin. Au moment où on considère le i-ème élément, les éléments qui le précèdent sont déjà triés. Pour faire l'analogie avec l'exemple du jeu de cartes, lorsqu'on est à la i-ème étape du parcours, le i-ème élément est la carte saisie, les éléments précédents sont la main triée et les éléments suivants correspondent aux cartes encore mélangées sur la table.

L'objectif d'une étape est d'insérer le i-ème élément à sa place parmi ceux qui précèdent. Il faut pour cela trouver où l'élément doit être inséré en le comparant aux autres, puis décaler les éléments afin de pouvoir effectuer l'insertion. En pratique, ces deux actions sont fréquemment effectuées en une passe, qui consiste à faire « remonter » l'élément au fur et à mesure jusqu'à rencontrer à un élément plus petit.

Voici une description en pseudo-code de l'algorithme présenté. Les éléments du tableau T sont numérotés de 0 à n-1.

        procédure tri_insertion(tableau T, entier n)            pour i de 1 à n - 1                x:= T[i]                j = i                tant que j > 0 et T[j - 1] > x                    T[j] = T[j - 1]                    j = j - 1;                T[j] = x      

Le tri par insertion est un tri stable (conservant l'ordre d'apparition des éléments égaux) et un tri en place (il n'utilise pas de tableau auxiliaire).

Complexité

La complexité du tri par insertion est Θ(n²) dans le pire cas et en moyenne, et linéaire dans le meilleur cas. Plus précisément :

1. Dans le pire cas, atteint lorsque le tableau est trié à l'envers, l'algorithme effectue de l'ordre de n²/2 affectations et comparaisons.
2. Si les éléments sont distincts et que toutes leurs permutations sont équiprobables, alors en moyenne, l'algorithme effectue de l'ordre de n²/4 affectations et comparaisons.
3. Si le tableau est déjà trié, il y a n-1 comparaisons et O(n) affectations.

La complexité du tri par insertion reste linéaire si le tableau est presque trié (par exemple, chaque élément est à une distance bornée de la position où il devrait être, ou bien tous les éléments sauf un nombre borné sont à leur place). Dans cette situation particulière, le tri par insertion surpasse d'autres méthodes de tri : par exemple, le tri fusion et le tri rapide (avec choix aléatoire du pivot) sont tous les deux en même sur une liste triée.