Tri rapide - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le tri rapide (en anglais quicksort) est un algorithme de tri inventé par C.A.R. Hoare en 1961 et fondé sur la méthode de conception diviser pour régner. Il est généralement utilisé sur des tableaux, mais peut aussi être adapté aux listes. Dans le cas des tableaux, c'est un tri en place mais non stable.
La complexité moyenne du tri rapide pour n éléments est proportionnelle à n log n, ce qui est optimal pour un tri par comparaison, mais la complexité dans le pire des cas est quadratique. Malgré ce désavantage théorique, c'est en pratique un des tris les plus rapides, et donc un des plus utilisés en pratique. Le pire cas est en effet peu probable lorsque l'algorithme est correctement implémenté. Le tri rapide ne peut cependant pas tirer avantage du fait que l'entrée est déjà presque triée. Dans ce cas particulier, il est plus avantageux d'utiliser le tri par insertion ou l'algorithme Smoothsort.
Description de l'algorithme
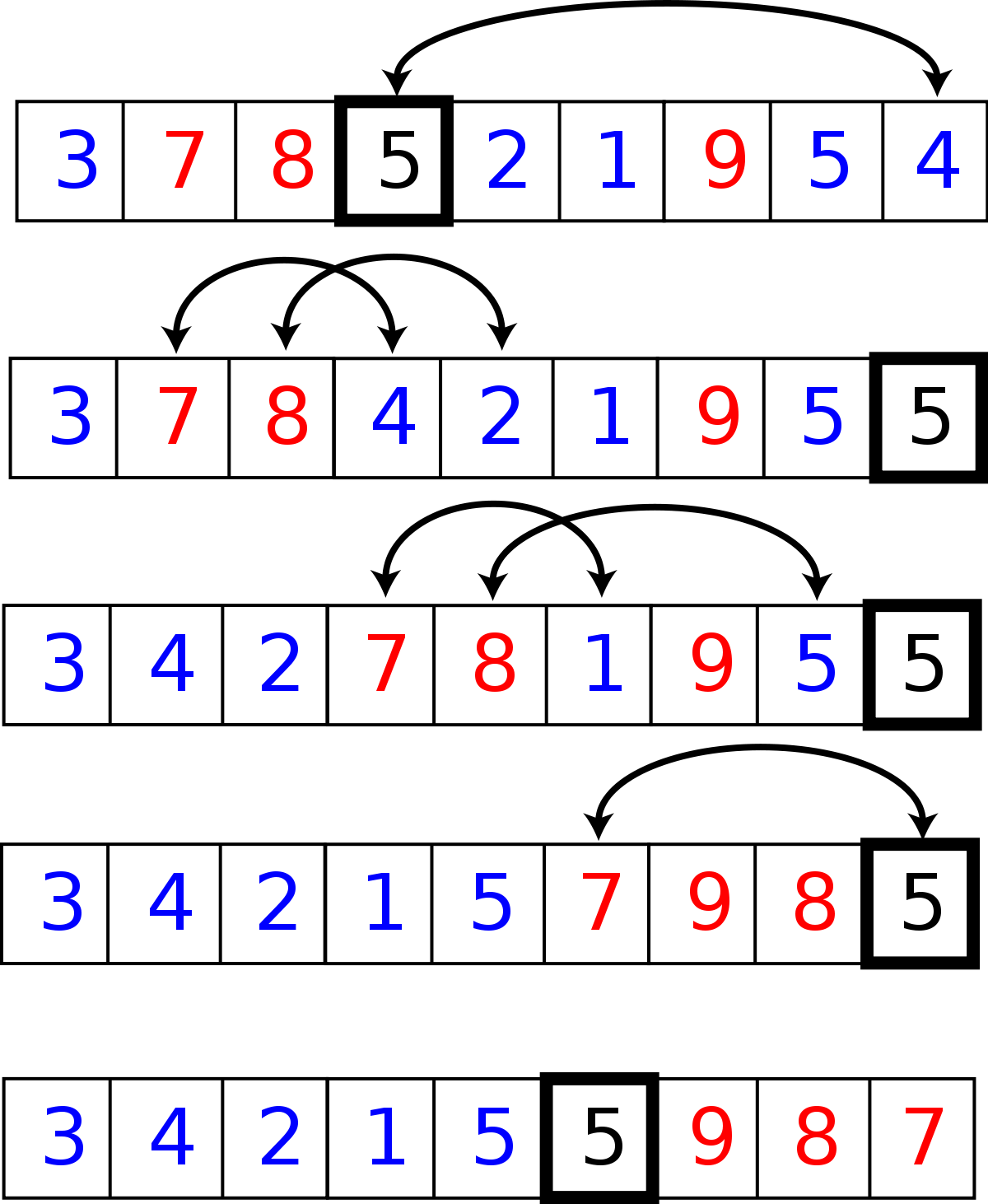
La méthode consiste à placer un élément du tableau (appelé pivot) à sa place définitive, en permutant tous les éléments de telle sorte que tous ceux qui lui sont inférieurs soient à sa gauche et que tous ceux qui lui sont supérieurs soient à sa droite. Cette opération s'appelle le partitionnement. Pour chacun des sous-tableaux, on définit un nouveau pivot et on répète l'opération de partitionnement. Ce processus est répété récursivement, jusqu'à ce que l'ensemble des éléments soit trié.
tri_rapide(tableau t, entier premier, entier dernier) début si premier < dernier alors pivot:= choix_pivot(t,premier,dernier) pivot:= partitionner(t,premier,dernier,pivot) tri_rapide(t,premier,pivot-1) tri_rapide(t,pivot+1,dernier) fin si fin
Choisir un pivot aléatoirement dans l'intervalle [premier, dernier] garantit l'efficacité de l'algorithme, mais il existe d'autres possibilités (voir la section « »).
Le partitionnement peut être fait en temps linéaire, en place. La mise en œuvre la plus simple consiste à parcourir le tableau du premier au dernier élément, en formant la partition au fur et à mesure : à la i-ème étape de l'algorithme ci-dessous, les éléments T[0],…,T[j-1] sont inférieurs au pivot, tandis que T[j],…,T[i-1] sont supérieurs au pivot.
partitionner(tableau T, premier, dernier, pivot) échanger T[pivot] et T[dernier] j:= premier pour i de premier à dernier - 1 si T[i] ≤ T[dernier] alors échanger T[i] et T[j] j:= j + 1 échanger T[dernier] et T[j] renvoyer j
Cet algorithme de partitionnement rend le tri rapide non stable : il ne préserve pas nécessairement l'ordre des éléments possédant une clef de tri identique. On peut résoudre ce problème en ajoutant l'information sur la position de départ à chaque élément et en ajoutant un test sur la position en cas d'égalité sur la clef de tri.
Le partitionnement peut poser problème si les éléments du tableau ne sont pas distincts. Dans le cas le plus dégénéré, c'est-à-dire un tableau de n éléments égaux, cette version de l'algorithme a une complexité quadratique. Plusieurs solutions sont possibles : par exemple se ramener au cas d'éléments distincts en utilisant la méthode décrite pour rendre le tri stable, ou bien utiliser un autre algorithme (voir la section « »).