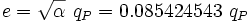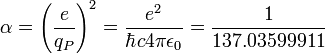Unités de Planck - Définition
La liste des auteurs de cet article est disponible ici.
Discussion
À l’échelle des constantes de Planck (en durée, longueur, densité ou température), il faut considérer à la fois les effets de la mécanique quantique et ceux de la relativité générale. Mais cela nécessite une théorie de la gravité quantique, qui n’existe pas encore.
La plupart des unités de Planck sont soit trop petites, soit trop grandes pour être utilisables en pratique, à moins de transporter des puissances de 10 dans les calculs. Elles souffrent aussi des incertitudes dans la mesure de certaines constantes sur lesquelles elles sont basées, notamment la constante de gravitation G qui a une incertitude de 1 sur 7000.
La charge de Planck n’a pas été définie ni proposée à l’origine par Planck. C’est une unité de charge qui a été définie de la même manière que les autres unités de Planck et qui est utilisée par les physiciens dans certaines publications. La charge élémentaire est ainsi définie par la charge de Planck de cette manière :
où
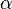
La valeur de la constante sans dimension de structure fine est définie par la quantité de charge, mesurée en unités naturelles (charge de Planck), que les électrons, protons, et autres particules chargée ont effectivement. Parce que la force électromagnétique entre deux particules est proportionnelle au produit des charges des deux particules (qui sont chacune, en unités de Planck, proportionnelles à
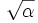
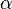
L’impédance de Planck est égale à l’impédance caractéristique du vide divisée par 4π : on a donc, en termes d’unités de Planck,
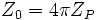
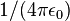
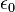
La découverte des unités naturelles de Planck
Max Planck a fait pour la première fois la liste de ses unités naturelles (et en a donné des valeurs remarquablement proches de celles que nous utilisons aujourd’hui) en mai 1899 dans un papier présenté à l’Académie des sciences de Prusse :
'Über irreversible Strahlungsvorgänge'. Sitzungsberichte der Preußischen Akademie der Wissenschaften, vol. 5, p. 479 (1899)
Au moment où il présenta ses unités, la mécanique quantique n’avait pas encore été découverte. Il n’avait pas encore découvert la théorie du rayonnement du corps noir (publiée pour la première fois en décembre 1900) dans laquelle la constante de Planck
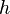
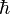
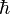
…ihre Bedeutung für alle Zeiten und für alle, auch außerirdische und außermenschliche Kulturen notwendig behalten und welche daher als »natürliche Maßeinheiten« bezeichnet werden können…
...Elle gardent nécessairement leur signification pour tous les temps et toutes les civilisations, mêmes extraterrestres et non humaines, et peuvent donc être désignées « unités naturelles »…