Constante de Planck - Définition

Introduction

Mécanique quantique

Postulats de la mécanique quantique Histoire de la mécanique quantique Concepts fondamentaux État quantique · Superposition · Observable · Intrication · Mesure · Principe d'incertitude · de correspondance · Dualité · Décohérence Expériences Fentes de Young · Expérience de Stern et Gerlach · Chat de Schrödinger · Gomme quantique · Paradoxe EPR · Téléportation quantique · Expérience d'Aspect Formalisme Notation Bra-Ket · Équation de Schrödinger · Matrice densité · Représentation de Schrödinger · de Heisenberg · d'interaction Statistiques Maxwell-Boltzmann · Échange · Fermi-Dirac · Fermion · Bose-Einstein · Boson Théories avancées Théorie quantique des champs · Axiomes de Wightman · Électrodynamique quantique · Chromodynamique quantique · Gravité quantique · Diagramme de Feynman Interprétations Problème de la mesure · Copenhague · Ensemble · Variables cachées · Transactionnelle · Mondes multiples · Histoires consistantes · Logique quantique · Réduction par l'observation (consciente) Physiciens Planck · de Broglie · Schrödinger · Heisenberg · Bohr · Pauli · Born · Dirac · von Neumann · Einstein · Bohm · Feynman · Everett · Penrose

Cette boîte : voir • disc. • mod.

En physique, la constante de Planck, notée h, est une constante utilisée pour décrire la taille des quanta. Elle joue un rôle central dans la mécanique quantique et a été nommée d'après le physicien Max Planck.

La constante de Planck, notée relie notamment l’énergie d’un photon à sa fréquence (lettre grecque nu) :

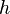
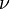
Valeur

Dans les unités SI, le CODATA de 2006 recommande la valeur suivante :

h ≈ 6,626 068 96×10^-34 J.s,

avec une incertitude standard de ±0,000 000 33×10^-34 J.s, soit une incertitude relative de 5,0×10^-8.

Première et seconde constantes de Planck de luminance

Dans la théorie des corps noirs, notamment pour l'expression de la luminance, on utilise deux autres constantes de Planck appelées C et C :

• C = 3,7415×10^-16  W⋅m²⋅sr^-1, soit C = 1 1 905×10^-16  W⋅m²
• C = 1 4 388×10^-2  m⋅K

Constante de Planck réduite ou de Dirac

La constante de Planck possède les dimensions d’une énergie multipliée par un temps. Il est possible d’écrire ces unités sous la forme d’une quantité de mouvement par une longueur (kg·mètre²·s^-1) c’est-à-dire les mêmes unités que le moment angulaire.

Une grandeur associée est le quantum d’action, également appelé constante de Planck réduite ou encore parfois constante de Dirac, notée ħ et prononcée « h barre » :

• Valeur en joules-secondes :

  ħ = h / 2 π ≈ 1,054 571 628×10^-34  J.s,

  avec une incertitude standard de ±0,000 000 053×10^-34  J.s.

• Valeur en électron-volts-secondes :

  ħ ≈ 6,582 118 99×10^-16  eV.s,

  avec une incertitude standard de ±0,000 000 16×10^-16  eV.s, soit une incertitude relative de 2,5×10^-8.

• Valeur en MeV-fermis :

  ħ c ≈ 197,326 963 1  MeV.fm,

  avec une incertitude standard de ±0,000 004 9  MeV.fm, soit une incertitude relative de 2,5×10^-8.

Interprétation physique

La constante de Planck est utilisée pour décrire les phénomènes de quantification qui se produisent avec les particules et dont certaines propriétés physiques ne prennent que des valeurs multiples de valeurs fixes au lieu d'un ensemble continu de valeurs possibles. Par exemple, l'énergie d'une particule est reliée à sa fréquence par :

.

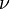
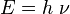
On retrouve de telles conditions de quantification dans toute la mécanique quantique. Par exemple, si est le moment angulaire total d’un système et le moment angulaire du système mesuré sur une direction quelconque, ces quantités ne peuvent prendre que les valeurs :

• , avec : 2j = 0, 1, 2, 3, 4, ...
• , avec : m = -j, -j+1, ..., j-1, j.

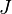
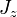
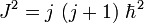
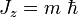
En conséquence, est parfois considérée comme un quantum de moment angulaire puisque le moment angulaire de n’importe quel système, mesuré par rapport à n'importe quel choix particulier d'axe, est toujours un multiple entier de cette valeur.

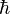
La constante de Planck réduite apparaît également dans les énoncés du principe d'incertitude de Heisenberg. L’écart type d’une mesure de position et celui d’une mesure de quantité de mouvement le long du même axe obéissent à la relation suivante :

.

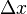
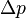
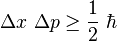
La constante de Planck réduite est également employée dans le système d’unités dit des unités de Planck.