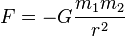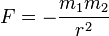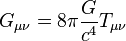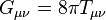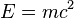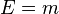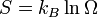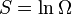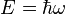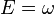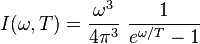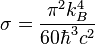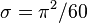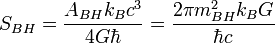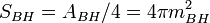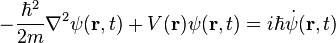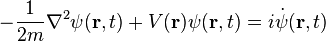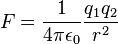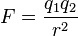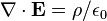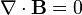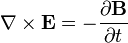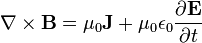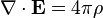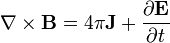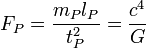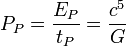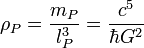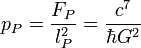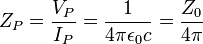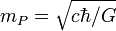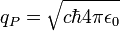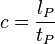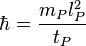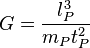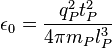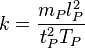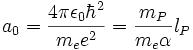Unités de Planck - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Les principales équations de la physique avec les unités de Planck - Unités de Planck : unités dérivées - Unités de Planck : unités de base - Les unités de Planck et l’invariance d’échelle de la nature - Discussion - La découverte des unités naturelles de Planck

Les principales équations de la physique avec les unités de Planck

Equations de la physique exprimées en unités de Planck
	Forme usuelle	Forme en unité sans dimension
Loi universelle de la gravitation de Newton	$F = - G \frac{m_1 m_2}{r^2}$	$F = - \frac{m_1 m_2}{r^2}$
Équation du champ gravitationnel d’Einstein (Relativité générale)	${ G_{\mu \nu} = 8 \pi {G \over c^4} T_{\mu \nu}} \$	${ G_{\mu \nu} = 8 \pi T_{\mu \nu} } \$
Formule Masse-Énergie d’Einstein	${ E = m c^2} \$	${ E = m } \$
Formule de l'entropie de Bolzmann	${ S = k_B \ln \Omega } \$	${ S = \ln \Omega } \$
Énergie d’un photon ou d’une particule de pulsation ω	${ E = \hbar \omega } \$	${ E = \omega } \$
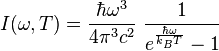
Loi de Planck	$I(\omega,T) = \frac{\hbar \omega^3 }{4 \pi^3 c^2}~\frac{1}{e^{\frac{\hbar \omega}{k_B T}}-1}$	$I(\omega,T) = \frac{\omega^3 }{4 \pi^3}~\frac{1}{e^{\omega/T}-1}$
Constante de Stefan-Boltzmann	$\sigma = \frac{\pi^2 k_B^4}{60 \hbar^3 c^2}$	$\ \sigma = \pi^2/60$
Formule de Bekenstein-Hawking de l'entropie des trous noirs	$S_{BH} = \frac{A_{BH} k_B c^3}{4 G \hbar} = \frac{2\pi m^2_{BH} k_B G}{\hbar c}$	$S_{BH} = A_{BH}/4 = 4\pi m^2_{BH}$
Équation de Schrödinger	$- \frac{\hbar^2}{2m} \nabla^2 \psi(\mathbf{r}, t) + V(\mathbf{r}) \psi(\mathbf{r}, t) = i \hbar \dot{\psi}(\mathbf{r}, t)$	$- \frac{1}{2m} \nabla^2 \psi(\mathbf{r}, t) + V(\mathbf{r}) \psi(\mathbf{r}, t) = i \dot{\psi}(\mathbf{r}, t)$
Loi de Coulomb	$F = \frac{1}{4 \pi \epsilon_0} \frac{q_1 q_2}{r^2}$	$F = \frac{q_1 q_2}{r^2}$
Equations de Maxwell	$\nabla \cdot \mathbf{E} = \rho / \epsilon_0$ $\nabla \cdot \mathbf{B} = 0 \$ $\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}} {\partial t}$ $\nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \epsilon_0 \frac{\partial \mathbf{E}} {\partial t}$	$\nabla \cdot \mathbf{E} = 4 \pi \rho \$ $\nabla \cdot \mathbf{B} = 0 \$ $\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}} {\partial t}$ $\nabla \times \mathbf{B} = 4 \pi \mathbf{J} + \frac{\partial \mathbf{E}} {\partial t}$

Unités de Planck : unités dérivées

nom	dimension	formule	valeur approchée, en système SI
force de Planck	force (MLT^-2)	$F_P = \frac{m_P l_P}{t_P^2} = \frac{c^4}{G}\;$	1.210 × 10⁴⁴ N
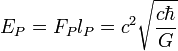
énergie de Planck	énergie (ML²T^-2)	$E_P = F_P l_P = c^2\sqrt{\frac{c \hbar}{G}}$	10¹⁹ GeV = 1.956 × 10⁹ J
puissance de Planck	puissance (ML²T^-3)	$P_P = \frac{E_P}{t_P} = \frac{c^5}{G}\;$	3.629 × 10⁵² W
densité de Planck	masse volumique (ML^-3)	$\rho_P = \frac{m_P}{l_P^3} = \frac{c^5}{\hbar G^2}\;$	5.1 × 10⁹⁶ kg/m³
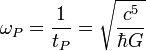
fréquence angulaire de Planck	fréquence (T^-1)	$\omega_P = \frac{1}{t_P} = \sqrt{\frac{c^5}{\hbar G}}\;$	1.855 × 10⁴³ rad/s
pression de Planck	pression (ML^-1T^-2)	$p_P = \frac{F_P}{l_P^2} = \frac{c^{7}}{\hbar G^2}\;$	4.635 × 10¹¹³ Pa
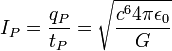
courant de Planck	courant électrique (QT^-1)	$I_P = \frac{q_P}{t_P} = \sqrt{\frac{c^6 4 \pi \epsilon_0}{G}}\;$	3.479 × 10²⁵ A
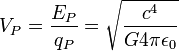
tension de Planck	tension (ML²T^-2Q^-1)	$V_P = \frac{E_P}{q_P} = \sqrt{\frac{c^4}{G 4 \pi \epsilon_0}}\;$	1.0432 × 10²⁷ V
impédance de Planck	résistance électrique (ML²T^-1Q^-2)	$Z_P = \frac{V_P}{I_P} = \frac{1}{4 \pi \epsilon_0 c} = \frac{Z_0}{4 \pi}\;$	2.9986 × 10¹ Ω

Unités de Planck : unités de base

nom	dimension	formule	valeur approchée, en système SI
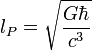
longueur de Planck	longueur (L)	$l_{P}= \sqrt{\frac{G\hbar}{c^3}}\;$	1.616 × 10^-35 m
masse de Planck	masse (M)	$m_{P} = \sqrt{c \hbar /G}\;$	2.177 × 10^-8 kg
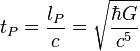
temps de Planck	temps (T)	$t_{P} = \frac{l_{P}}{c} = \sqrt{\frac{\hbar G}{c^5}}\;$	5.391 × 10^-44 s
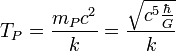
température de Planck	température (Θ)	$T_{P} = \frac{m_{P} c^2}{k} = \frac{\sqrt{c^5 \frac{\hbar}{G}}}{k}$	1.415 × 10³² K
charge de Planck	charge électrique (Q)	$q_{P} = \sqrt{c \hbar 4 \pi \epsilon_0 }\;$	1.875 × 10^-18 C

Les trois constantes de la physique sont ainsi exprimées simplement en utilisant les unités de base de Planck :

Les unités de Planck et l’invariance d’échelle de la nature

D’après Duff dans Comment on time-variation of fundamental constants et Duff, Okun et Veneziano dans Trialogue on the number of fundamental constants (The operationally indistinguishable world of Mr. Tompkins), si toutes les quantités physiques (la masse et les autres propriétés des particules) étaient exprimées en unités de Planck, ces quantités seraient des nombres sans dimension (une masse divisée par la masse de Planck, une longueur divisée par la longueur de Planck, etc.). Les seules quantités que nous mesurons finalement dans les expériences en physique ou par notre perception de la réalité sont des nombres sans dimension. En effet, lorsqu’on mesure habituellement une longueur avec une règle ou un mètre-ruban, on compte en fait les marques faites d’après un étalon ; autrement dit, on mesure la longueur relative à cette longueur de référence. Il en va de même pour les expériences en physique, où toutes les quantités physiques sont mesurées relativement à d’autres grandeurs physiques dimensionnées. 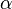Nous pourrions constater des changements si certaines quantités sans dimension comme $\alpha \$ ou le rapport des masses proton/électron étaient modifiées (la structure atomique changerait), mais si toutes les quantités physiques sans dimension restaient constantes, nous ne pourrions pas dire si une quantité dimensionnée, comme la vitesse de la lumière, c, a changé. Et, en effet, le concept de Tompkins devient insignifiant dans notre existence si une quantité dimensionnée comme c change, même énormément.

Si la vitesse de la lumière c était soudainement divisée par deux et changée en c/2, mais en gardant inchangées toutes les constantes adimensionnées, alors la Longueur de Planck serait augmentée d’un rapport de √8 du point de vue de certains observateurs extérieurs non touchés par le changement. Mais comme la taille des atomes (approximativement le rayon de Bohr) est liée à la longueur de Planck par une constante sans dimension :

alors les atomes seraient plus gros (dans chaque dimension) par √8, chacun de nous serait plus grand de √8, et ainsi nos règles à mesurer seraient plus grandes (et plus épaisses, et plus larges) d’un rapport √8, et nous ne saurions rien de ce changement.

Le tic-tac de nos montres serait plus lent d’un rapport √32 (du point de vue de l’observateur extérieur non concerné par les changements), parce que le temps de Planck aurait augmenté de √32, mais nous ne verrions pas la différence. Cet observateur extérieur hypothétique pourrait constater que la lumière se déplace à la moitié de son ancienne vitesse (de même que toutes les vitesses), elle parcourrait toujours 299 792 458 de nos nouveaux mètres par une de nos nouvelles secondes. Nous ne verrions aucune différence.

Ceci contredit conceptuellement George Gamow dans Monsieur Tompkins qui suppose que si une constante universelle comme c changeait, nous remarquerions facilement la différence. Nous devons maintenant lui demander : Comment mesurerions-nous la différence si nos références de mesure changeaient de la même manière ?

Introduction

Discussion

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Existe-t-il des mélodies naturelles ? 🎶

Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

Page générée en 0.138 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise