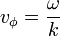Vitesse d'une onde - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Vitesse de phase - Vitesse de groupe

Introduction

Une onde est une perturbation qui se déplace dans un milieu. Il est possible de lui associer deux vitesses d'onde.

Dans un milieu homogène, la propagation dans une direction donnée d'une onde monochromatique, ou sinusoïdale, se traduit par une simple translation de la sinusoïde à une vitesse appelée vitesse de phase ou célérité. Les ondes plus compliquées peuvent généralement être considérées comme des sommes de sinusoïdes de différentes fréquences ou pulsations (voir Analyse spectrale). Si la vitesse de phase ne dépend pas de la fréquence, l'onde résultante subit aussi une translation globale sans déformation. Dans le cas contraire, les composantes se dispersent. On peut alors souvent identifier des groupes d'ondes dont le maximum se déplace à une vitesse de groupe différente des célérités des composantes.

Vitesse de phase

Vitesse de phase d’une onde monochromatique. Le point rouge, localisé sur l’onde à une phase donnée (la crête, dans cet exemple), avance à la vitesse de phase.

La vitesse de phase d'une onde est la vitesse à laquelle la phase de l'onde se propage dans l'espace. Si l'on sélectionne n'importe quel point particulier de l'onde (par exemple la crête), il donnera l'impression de se déplacer dans l'espace à la vitesse de phase. La vitesse de phase s'exprime en fonction de la pulsation de l'onde ω et du vecteur d'onde k :

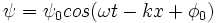
En effet, soit une onde monochromatique $\psi = \psi_{0}cos(\omega t - kx+ \phi_{0})\,$ , plaçons nous sur une surface d'onde, i.e. l'ensemble des points ayant la même valeur de $\psi\,$ , par conséquent la même valeur de la phase $\phi\,$ , c'est le plan de phase. Le plan de phase $\phi\,$ est en $x\,$ au temps $t\,$ :

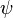
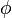
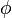
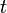
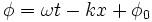
$\phi = \omega t - kx+ \phi_{0}\,$

et en $x+dx\,$ au temps $t+dt\,$ :

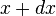
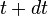
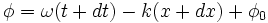
$\phi = \omega (t+dt) - k(x+dx)+ \phi_{0}\,$

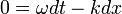
d'où par différence $0 = \omega dt - k dx\,$

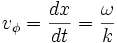
i.e. $v_{\phi}=\frac{dx}{dt}=\frac{\omega}{k}\,$

Cas des ondes électromagnétiques

Dans ce cas la vitesse de phase, égale à une constante $c$ dans le vide, diminue dans un milieu transparent. Cette diminution est caractérisée par l'indice du milieu :

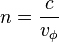
$n = \frac{c}{v_{\phi}}\,$

De plus, le milieu est dispersif : cet indice dépend du nombre d'onde (donc de la longueur d'onde), ce qui conduit à introduire la notion de vitesse de groupe.

La vitesse de phase d'une onde électromagnétique peut être supérieure à la vitesse de la lumière dans le vide dans certaines circonstances (en particulier lorsque l'indice de réfraction du matériau est plus petit que 1 à certaines fréquences. Typiquement, on observe ce phénomène pour des rayons X) mais cela n'implique pas un transfert d'énergie ou d'information à une vitesse supérieure à celle de la lumière. En effet, une onde se déplace à sa vitesse de phase dans un groupe, qui lui se déplace à la vitesse de groupe de l'onde (voir ci-dessous). Les fronts d'onde se déplaçant à la vitesse de phase le font d'un front de la vitesse de groupe, au suivant. Cependant, les fronts d'onde à la vitesse de phase ne peuvent pas exister en dehors de fronts d'onde qui voyagent à la vitesse de groupe. L'onde totale, c'est-à-dire le transfert d'information, s'effectue donc toujours à la vitesse la plus lente des deux. 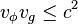Or comme $v_{\phi}v_g \leq c^2$ (voir plus bas) cette vitesse est inférieure à la vitesse de la lumière dans le vide. Une justification mathématique simple à cette affirmation est que l'onde totale est le produit d'une onde se déplaçant à $v φ$ avec une onde se déplaçant à $v g$ . Si l'un des deux est nul (par exemple si l'on se trouve dans une région ou que les fronts d'onde se déplaçant à $v g$ n'ont pas eu le temps d'atteindre) le produit des deux, c'est-à-dire l'onde totale, doit aussi être nul. L'information se déplace donc toujours à la vitesse la plus lente des deux : $v i n f o r m a t i o n = min(v g, v φ)$ .