Vitesse d'une onde - Définition

Vitesse de groupe

Vitesses de phase et de groupe d’une superposition de deux ondes monochromatiques. Le point rouge avance à la vitesse de phase et les points verts à la vitesse de groupe. Dans cet exemple, la vitesse de phase vaut le double de la vitesse de groupe.

D'après ce qui précède, la vitesse de phase d'une onde monochromatique est égale au rapport de sa pulsation à son nombre d'onde. Considérons le cas le plus simple de deux ondes superposées de pulsations voisines et d'amplitude unité (les phases qui n'interviennent pas sont ignorées) :

Selon la trigonométrie, une somme de cosinus se transforme en un produit de cosinus :

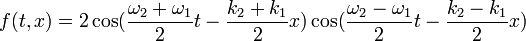
Il apparaît un phénomène de battement dans lequel une sinusoïde de caractéristiques proches de celles des deux composantes, est modulée par une sinusoïde de plus basse fréquence dont la célérité est . Cette quantité représente la vitesse de groupe. La vitesse de phase est la célérité de la sinusoïde modulée : Lorsque les deux fréquences de départ sont voisines, celle-ci est approximativement égale à

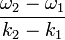
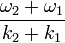
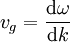
Dans le cas général de plus de deux ondes monochromatiques superposées, cette vitesse de groupe concerne une enveloppe plus compliquée qu'une sinusoïde.

La fonction qui exprime la pulsation en fonction du nombre d'onde définit la relation de dispersion. Lorsque la pulsation est directement proportionnelle au nombre d'onde, ce qui signifie que la vitesse de phase est indépendante de la pulsation, alors la vitesse de groupe est égale à cette vitesse de phase commune. Dans le cas contraire, l'enveloppe de l'onde se déforme au cours de la propagation.

Cas des ondes électromagnétiques

Dans le cas d'une onde électromagnétique, la vitesse de phase et la vitesse de groupe sont liées par la relation (qui fonctionne à basse fréquence uniquement) :

avec c vitesse de la lumière dans le vide.

La dispersion due à la vitesse de groupe est un effet important pris en compte pour la propagation d'informations par fibres optiques.

La vitesse de groupe est généralement présentée comme la vitesse à laquelle l'énergie ou l'information est transportée par une onde. Cette description est généralement valide, bien qu'il soit tout de même possible de réaliser des expériences dans lesquelles la vitesse d'impulsions laser envoyées dans des matériaux spécifiques soit supérieure à la vitesse de transmission du signal.