Transitivité (mathématiques) - Définition
En mathématiques, la transitivité est une propriété éventuelle d'une relation binaire. Une relation binaire
-
![\forall x, y, z \in E\left[(x \mathcal{R} y \and y \mathcal{R} z) \implies x \mathcal{R} z\right]](https://static.techno-science.net/illustration/Definitions/autres/8/86fbf7a325c8a1615bced0010ae3e7bd_dab0cd0bf49cd1937ab1ed1bc54066fd.png)
![\forall x, y, z \in E\left[(x \mathcal{R} y \and y \mathcal{R} z) \implies x \mathcal{R} z\right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/8/86fbf7a325c8a1615bced0010ae3e7bd_dab0cd0bf49cd1937ab1ed1bc54066fd.png)
Si l'amitié était transitive, on pourrait affirmer " Tous les amis de mes amis sont mes amis."
On en déduit qu'une relation sur E n'est pas transitive si et seulement s'il existe un triplet d'éléments de E qui fournit un contre-exemple à la transitivité : x et y sont en relation, ainsi que y et z, mais pas x et z. Plus formellement :
-
![\exists x, y, z \in E\left[x \mathcal{R} y \and y \mathcal{R} z \and \lnot(x\mathcal{R}z)\right]](https://static.techno-science.net/illustration/Definitions/autres/b/b567fdbd7832f7de8a211e41e22fd529_bd5c77be5dbe57c11430dafb8236e60b.png)
![\exists x, y, z \in E\left[x \mathcal{R} y \and y \mathcal{R} z \and \lnot(x\mathcal{R}z)\right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/b/b567fdbd7832f7de8a211e41e22fd529_bd5c77be5dbe57c11430dafb8236e60b.png)
On dit alors que la relation binaire
-
![\forall x, y, z \in E \left[(x \mathcal{R} y \and y \mathcal{R} z) \implies\lnot(x \mathcal{R} z)\right]](https://static.techno-science.net/illustration/Definitions/autres/6/6951c8ce600e4cd5383572cd8547a314_148314d3082a06548533cd801e52ea28.png)
![\forall x, y, z \in E \left[(x \mathcal{R} y \and y \mathcal{R} z) \implies\lnot(x \mathcal{R} z)\right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/6/6951c8ce600e4cd5383572cd8547a314_148314d3082a06548533cd801e52ea28.png)
On dit parfois d'une telle relation qu'elle est anti-transitive (cette propriété est moins utile et moins courante que la transitivité, le vocabulaire n'est pas forcément bien établi). Remarquez que les propriétés de non-transitivité et d'anti-transitivité ne sont pas comparables (acune des deux n'entraîne l'autre), et qu'une relation, même non vide, peut très bien être transitive et anti-transitive (il suffit qu'il n'y ait pas de triplet (x, y z) vérifiant x R y et y R z).
Exemples
- Les relations = ,
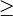
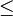
- La relation de parallélisme est transitive : si une droite D est parallèle à D', elle-même parallèle à D", alors D est parallèle à D". Il en est de même pour toute relation d'équivalence.
- De même, les relations d'ordre sont transitives. Par exemple,
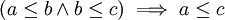
- Ainsi, on dit de la relation de congruence qu'elle est transitive dans
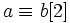
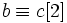
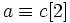
Exemple de non-transitivité
- La relation
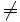
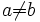
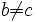
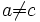
Exemple d'anti-transitivité
- La relation "est le père de" est anti-transitive : si (a est le père de b) et (b est le père de c), alors (a N'est PAS le père de c).
