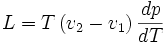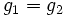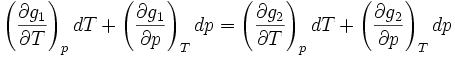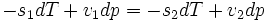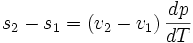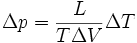Formule de Clapeyron - Définition

La formule de Clapeyron ou relation de Clausius-Clapeyron est une formule générale permettant de calculer la chaleur latente L d'un changement de phase de la matière en fonction des volumes molaires du corps dans les deux phases à l'équilibre et connaissant la courbe de changement de phase donnant la pression en fonction de la température. Ou de façon inverse, le changement de pression ou de température lors d'un changement de phase si on connaît les autres variables.

Définition

Exemple de diagramme de phase de l'eau où les lignes représentent la formule de Clapeyron

La formule est :

Cette formule est valable dans le cas d'une transition de phase du premier ordre.

(Pour les transitions de phase du deuxième ordre voir les formules d'Ehrenfest)

• Température à laquelle se produit le changement de phase.
• volume massique respectif du corps dans les deux phases à l'équilibre.
• dérivée de la pression par rapport à la température.

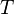
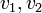
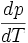
Démonstration de la formule

Nous savons que lorsque deux phases coexistent pour un corps pur, le potentiel chimique de ce corps est le même dans chacune des deux phases.

En différentiant, on obtient :

Qui s'écrit :

C’est-à-dire :

D'autre part, considérons la relation de définition de l'enthalpie libre :

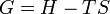
Les deux phases étant à l'équilibre et la température étant constante, on obtient en différenciant :

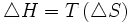
Pour une mole de produit, on obtient bien :

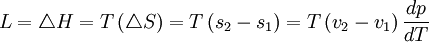
Applications

Problème pratique

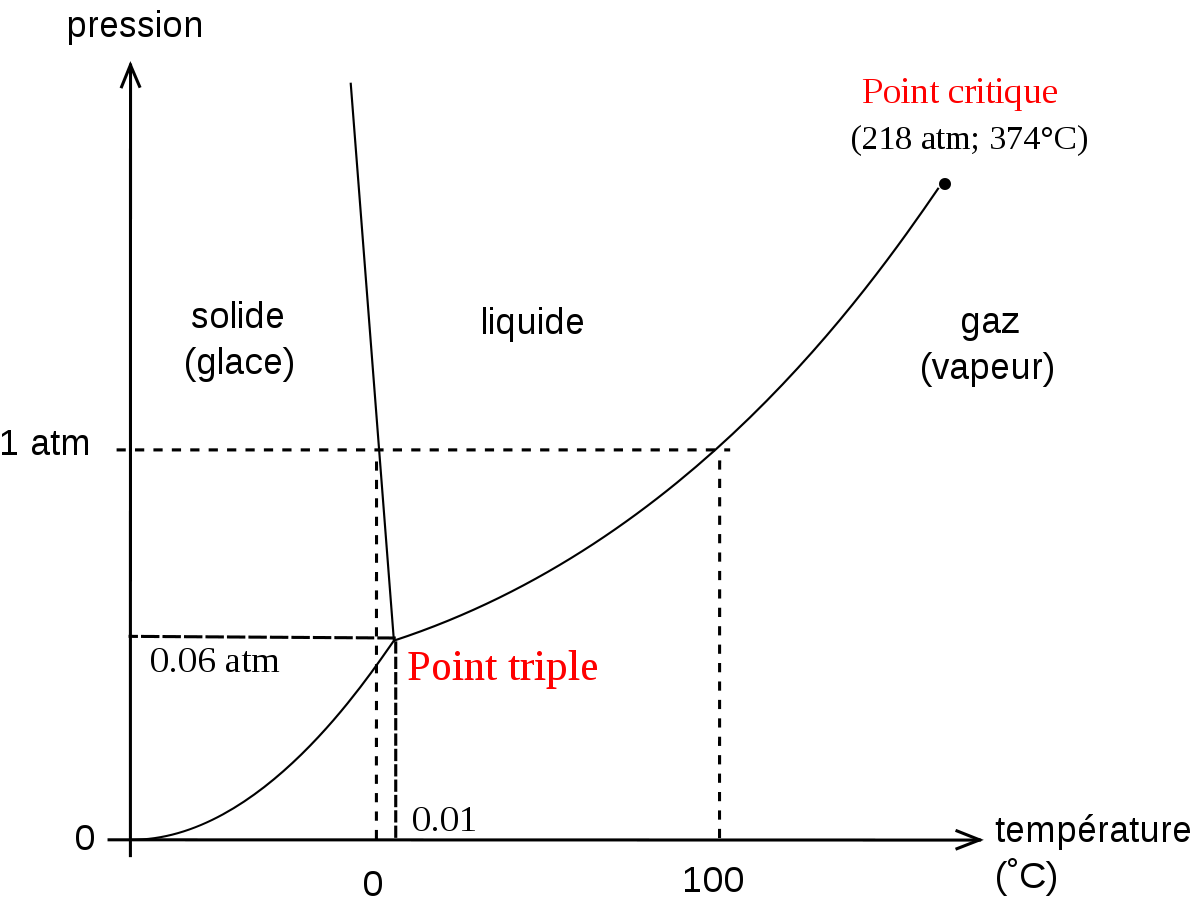
La relation est utilisée pour savoir s'il y aura changement de phase ou non selon les conditions de pression et de température. Par exemple, elle est souvent utilisée pour expliquer ce qui permet le patinage sur glace: l'augmentation de pression du patineur fait fondre une mince couche de glace sous le patin.

Si T = −2 °C, en utilisant Clausius-Clapeyron pour calculer le changement de pression nécessaire, nous devons avoir :

En utilisant :

L = 3.34*10⁵ J/kg, T=271K, ΔV = -9.05 *10^-5m3/kg,

et

ΔT = 2K,

nous obtenons

Δp = 27.2 MPa.

C'est équivalent au poids d'un lutteur de sumo (masse = 150 kg) se tenant sur un talon aiguille (surface = 0.5 cm²)!

Ça ne semble pas la seule raison!

Météorologie

En météorologie, la relation de Clausius-Clapeyron est utilisée couramment dans les diagrammes thermodynamiques comme les téphigrammes, Skew-T et émagrammes pour le calcul des énergies de changement de phases de l'eau atmosphérique. Sur un tel diagramme de pression versus température (P-T), la ligne séparant les deux phases est connue comme la courbe de coexistence: dP/dT.

Ce qui est surtout important en météorologie est la pression de saturation de la vapeur d'eau '''e_s''' et la relation devient alors:

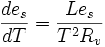
où R_v est la constante des gaz parfaits individuels (pour l'eau 1850 J/Kg-K)