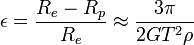Aplatissement - Définition
L'aplatissement d'une planète est une mesure de son " ellipticité "; une sphère a un aplatissement de 0, alors qu'un disque infiniment mince a un aplatissement de 1.
Une planète en rotation a une tendance naturelle à s'aplatir, l'effet centrifuge créant un " bourrelet équatorial ". Mathématiquement, l'aplatissement est donné par :
où Re et Rp sont les rayons équatorial et polaire de la planète, respectivement. L'approximation, valide dans le cas d'une planète fluide de densité uniforme, est fonction de la constante de gravitation universelle, G, de la période de rotation T et de la densité ρ.