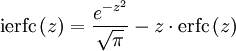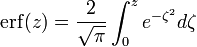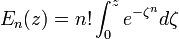Fonction d'erreur - Définition
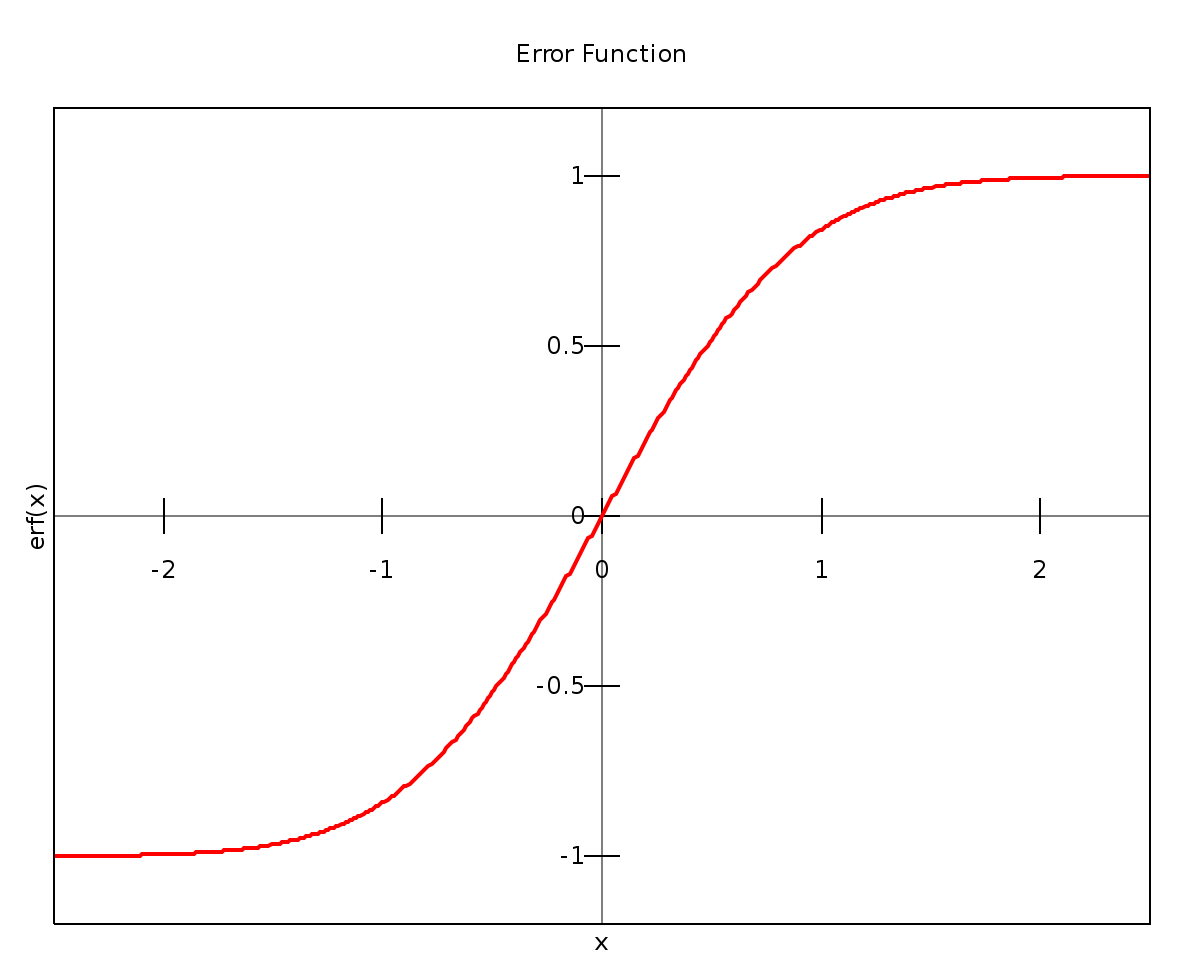
En mathématiques, la fonction d'erreur (aussi appelée fonction d'erreur de Gauss) est une fonction utilisée en analyse. Cette fonction se note erf et fait partie des fonctions spéciales.
La probabilité pour qu'une variable normale centrée réduite prenne une valeur dans l'intervalle [-z, z] est
-
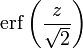
c'est la distribution normale.
Elle intervient, par exemple dans les solutions de l'équation de la chaleur, quand les conditions aux bords sont données par la fonction de Heaviside.
L'intégrale ne peut être obtenue à partir d'une formule fermée mais par un développement en série entière intégré termes à termes. Il existe des tables donnant des valeurs des intégrales, comme fonctions de z.
Il arrive que la fonction plus générale En définie par :
soit utilisée et E2 est appelée erreur intégrale.
D'autres fonctions d'erreurs utilisées en analyse, notamment :
- La fonction d'erreur complémentaire notée erfc et définie par :
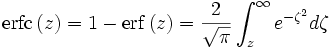
- La fonction ierfc, intégrale de la fonction d'erreur complémentaire erfc :